

 Vol. 38 (Nº 60) Año 2017. Pág. 2
Vol. 38 (Nº 60) Año 2017. Pág. 2
Alcides José TRZASKACZ 1; Karolina Barone Ribeiro da Silva HRENTCHECHEN 2
Recibido: 06/08/2017 • Aprobado: 03/09/2017
RESUMO: Este artigo teve como objetivo elaborar uma história dos números irracionais partindo de fontes históricas da matemática como livros da história e livros didáticos. O surgimento dos irracionais deu-se pela necessidade de calcular a diagonal do quadrado de lado 1. A aceitação destes números na época, teria custado a vida de Hipasus de Metapontum, por revelar a irracionalidade de √2, negando a filosofia pitagórica de que fenômenos do universo poderiam ser reduzidos em números inteiros. |
ABSTRACT: This article aims to elaborate a history of irrational numbers from historical sources of mathematics such as history books and textbooks. The emergence of the irrational was due to the necessity of calculating the diagonal of the square of side 1. The acceptance of these numbers at the time would have cost the life of Hipasus of Metapontum, for revealing the irrationality of √2, denying the Pythagorean philosophy that phenomena of the universe could be reduced in whole numbers. |
No presente artigo são apontados resultados obtidos em um projeto de pesquisa (Iniciação Científica), desenvolvido pelo primeiro autor, sob orientação do segundo, no âmbito do Departamento de Matemática da UNICENTRO (campus Irati – PR).
No curso de licenciatura em Matemática da UNICENTRO, caracterizado por formar professores para a Educação Básica, deve-se levar em consideração, dentre outros documentos, as Diretrizes Curriculares da Educação Básica do Estado do Paraná (PARANÁ, 2008), que propõem os seguintes conteúdos estruturantes para as escolas da Rede Pública Estadual: Números e Álgebra, Grandezas e Medidas, Geometrias, Funções e Tratamento da Informação.
Para o 8º ano do Ensino Fundamental, o tópico Números e Álgebra se desdobra em: números racionais e irracionais, sistemas de equações do 1º grau, potências, monômios e polinômios, produtos notáveis. O interesse da pesquisa aqui descrita está na segunda parte do primeiro item. Em relação a esse tema, as Diretrizes afirmam que se espera que o aluno
Reconheça números irracionais em diferentes contextos;
Realize operações com números irracionais;
Compreenda, identifique e reconheça o número π (pi) como um número irracional especial. (PARANÁ, 2008, p. 78)
Ao longo dos anos, estudantes têm apresentado dificuldades com os números irracionais. Algumas delas estão relatadas, por exemplo, em Santos (2007), Silva e Penteado (2009) e em Broetto (2013). Segundo os três últimos autores, os problemas com irracionais chegam ao ponto de alguns alunos acharem que tais números são apenas aqueles que podem ser representados como raízes quadradas não exatas. Para Pasquini e Pereira (2010), algumas das dúvidas geradas nos alunos sobre o tema são resultantes do modo como ele é apresentado nos livros didáticos, que muitas vezes não relacionam números irracionais ao conceito de incomensurabilidade.
Para que o professor esteja preparado para corrigir eventuais equívocos na apresentação dos irracionais nos livros didáticos e sanar algumas dúvidas dos alunos quanto ao tema, é necessário recorrer à história da matemática, como indicam os Parâmetros Curriculares Nacionais (BRASIL, 1997, p. 39, grifo nosso):
Ao longo do ensino fundamental os conhecimentos numéricos são conhecidos e assimilados pelos alunos num processo dialético, em que intervêm como instrumentos eficazes para resolver determinados problemas e como objetos que serão estudados, considerando-se suas propriedades, relações e o modo como se configuram historicamente.
Nesse processo, o aluno perceberá a existência de diversas categorias numéricas criadas em função de diferentes problemas que a humanidade teve que enfrentar – números naturais, números inteiros positivos e negativos, números racionais (com representações fracionárias e decimais) e números irracionais.
Diante do exposto anteriormente se justifica o interesse por elaborar uma história dos números irracionais a partir de fontes históricas da matemática.
A modalidade de pesquisa utilizada para atingir o objetivo descrito anteriormente foi a bibliográfica.
A pesquisa de cunho bibliográfico, por suas características, possibilita efetivar um estudo de caráter correlacional, haja vista que
[...] explica um problema, fundamentando-se apenas nas contribuições secundárias, ou seja, nas informações e dados extraídos de livros de leitura corrente e de referências, de revistas impressas e virtuais, material audiovisual, entrevistas, documentos, etc. de diferentes autores que versam sobre o tema selecionado para o estudo (REIS, 2008, p.51).
A finalidade da pesquisa bibliográfica, segundo Pádua (2004, p.55), é “colocar o pesquisador em contato com o que já se produziu e registrou a respeito do seu tema de pesquisa”.
Inicialmente foram efetuadas seleção e análise de livros de história da matemática, sendo, Berlinghoff e Gouvêa (2008), Boyer (1974), Cajori (2007), Contador (2006), Eves (2004), Garbi (2006) e Roque (2012), para buscar explicações a fim de atender aos seguintes objetivos específicos: investigar problemas que desencadearam o “surgimento” dos números irracionais; estudar a aceitação dos irracionais na comunidade matemática à medida que novos números com esta classificação eram “descobertos”; determinar o primeiro irracional conhecido e alguns que o sucederam; compreender o porquê do termo “irracional” e elencar os irracionais mais conhecidos da história da matemática. Outras fontes utilizadas com o mesmo propósito foram Maor (2008), que trata especificamente da história do número e, bem como Mlodinow (2010), acerca da história da geometria.
Posteriormente foram consultados livros didáticos (incluindo o manual do professor) utilizados na Educação Básica: Andrini e Vasconcellos (2012), Bianchinni (2011), Centurión e Jakubovic (2012), Dante (2012), Leonardo (2010), Mori e Onaga (2012) e Souza e Pataro (2012) do Ensino Fundamental, e Iezzi (2010/2013), Smole (2010)e Ribeiro (2010) do Ensino Médio, para verificar como os irracionais eram apresentados, observando a coerência entre as informações tratadas e o contido nos livros de história da matemática.
Números irracionais são aqueles que não podem ser escritos sob a forma de razão entre dois números inteiros. Segundo a história que se tem sobre tais números Pitágoras afirmava, devido a sua prática de associar figuras geométricas com números, que alguns comprimentos não poderiam ser expressos por um número inteiro.
Segundo Mlodinow (2010, p. 37):
Os pitagóricos chamaram tais comprimentos de alogon, “não racionais”, que hoje traduzimos como “irracional”. Todavia a palavra alogon tinha duplo sentido: significava também “não deve ser falado”.
Credita-se ao pitagórico Hipasus de Metapontum (último quarto do quinto século a.C.) tal descoberta, sendo que ela produziu uma crise nos fundamentos da matemática grega e na escola pitagórica, pois na sua filosofia tudo dependia dos números inteiros.
De acordo com Boyer (1974, p. 53):
De Hipasus de Metapontum (ou Crotona) aproximadamente contemporâneo de Filolaus, diz-se ter sido inicialmente um pitagórico, que foi expulso da confraria. Uma estória diz que os pitagóricos lhe erigiriam um túmulo, como se estivesse morto, outra que sua apostasia foi punida pela morte num naufrágio, sendo esta a punição por ter declarado tal descoberta.
Encontra-se em Contador (2008) informações análogas às de Boyer, porém em Cajori (2007), a teoria das quantidades irracionais é atribuída aos pitagóricos por Eudemo e Hipasso teria sido o primeiro a revelar a descoberta dos irracionais que os pitagóricos tinham em segredo, tendo como consequência a morte em um naufrágio.
Em Garbi (2006, p.32) encontra-se o seguinte relato:

A descoberta da existência de grandezas incomensuráveis é a mais importante contribuição matemática atribuída aos pitagóricos. Eles provaram que a razão entre o lado e a diagonal de um quadrado não pode ser a razão de quaisquer dois números inteiros, sendo chamados segmentos dessa espécie de incomensuráveis e de irracional a razão desses segmentos (CAJORI,2007).

Os irracionais fazem parte de outros problemas matemáticos, entre eles, a Duplicação do Cubo. O período de 443 a.C. a 429 a.C. é denominado como Época de Péricles, homem de caráter incorruptível, que governou Atenas buscando uma democracia ideal, em que houvesse equilíbrio entre interesses do estado e dos cidadãos. A origem deste problema pode estar relacionada à mitologia grega pela qual o surgimento de uma peste teria dizimado 75% da população de Atenas. Em busca de solucionar o problema, que teria feito também Péricles (500 a.C. a 429 a.C.) uma de suas vítimas, os moradores de Atenas enviaram ao templo de Apolo uma delegação em busca de ajuda. Havendo lá um altar em forma de cubo a divindade fez um pedido em troca do fim da peste: “erguei-me um altar igual ao dobro do já existente e a peste cessará” (CONTADOR, 2008, p. 233). A princípio um problema fácil de ser resolvido, no entanto, o cubo tinha arestas iguais a 1m, então seu volume se calcula por V=1x1x1=1m3 e para duplicá-lo seria simples, sendo necessário apenas dobrar suas arestas de tamanho. Porém seu volume se daria por V=2x2x2=8m3, que é quatro vezes maior do que o pedido. Assim sendo, qual o tamanho da aresta para que o cubo tenha o volume igual a 2m?
Contador (2008, p.234) diz:
No plano duplica-se um quadrado e no espaço é impossível duplicar um cubo. Hoje essa resposta não é difícil de ser dada, acontece que para duplicar um cubo precisamos achar uma aresta a ou um número que satisfaça a condição a.a.a=2 ou a3=2, a=![]() , e novamente vem daí que a=1,2 é pequeno e a=1,3 é grande. Nossa única alternativa é mostrar a impossibilidade de calcular o comprimento desta aresta, ou seja, mostrar que o número procurado é irracional. Segundo o problema a3=2, se a fosse racional poderíamos escrevê-lo sob a forma de fração irredutível
, e novamente vem daí que a=1,2 é pequeno e a=1,3 é grande. Nossa única alternativa é mostrar a impossibilidade de calcular o comprimento desta aresta, ou seja, mostrar que o número procurado é irracional. Segundo o problema a3=2, se a fosse racional poderíamos escrevê-lo sob a forma de fração irredutível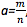 , isto é, n e m não possuem mais divisor comum.
, isto é, n e m não possuem mais divisor comum.
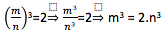

O mesmo relato do problema da duplicação do cubo é encontrado em Eves (2004), no qual há uma segunda possibilidade sobre o seu surgimento. O rei Minos, que era filho de Zeus, descontente com o tamanho do túmulo, construído em forma cúbica, ordenou por sugestão de Eurípedes, poeta sem conhecimento matemático, que fosse duplicado, pois ele teria ficado pequeno para seu filho Glauco. Toda duplicação de volume de um sólido tornou-se um desafio para que sua forma original fosse mantida.
O número π (letra grega que se pronuncia pi) surgiu pela necessidade de se calcular a área ou volume de figuras geométricas. Ele é obtido pela razão entre o comprimento e o raio de uma circunferência, ou pela razão entre a área de um círculo e a área de um quadrado que tem seu raio como lado.
Esse número não nasceu com o nome de π (pi), sendo muitos anos mais tarde batizado por William Jones.
Berlingoff e Gouvêa (2008, p. 110) afirmam que
1706- William Jones, um matemático britânico, foi o primeiro a usar uma letra grega π como o nome desse número. O símbolo foi adotado pelo grande matemático suíço Leonard Euler em suas publicações nas décadas de 1730 e 1740 e, pelo final do século, ela se tornara o nome comum dessa constante.
Segundo Contador (2008), antes ainda de Arquimedes, o Papiro de Rhind (1650 a.C.) mostra um procedimento para calcular a área de um círculo que usava a constante 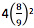 , o papiro não dá o valor de π (pi), mas fornece uma regra para calcular a área de um corpo circular e ainda mostra problemas envolvendo áreas de círculo no qual o valor utilizado para π (pi) é de 3,16.
, o papiro não dá o valor de π (pi), mas fornece uma regra para calcular a área de um corpo circular e ainda mostra problemas envolvendo áreas de círculo no qual o valor utilizado para π (pi) é de 3,16.
Berlingoff e Gouvêa (2008, p. 111) informam que
Mais ou menos em 1765 (quando os Estados Unidos estavam caminhando para a guerra revolucionária), um matemático alemão chamado Johann Lambert demonstrou que π é um número irracional; isto é, não pode ser expresso exatamente como uma fração ordinária (ou seja, a razão entre dois números inteiros)
Por fim, Contador (2008, p. 266) explica que
Mais tarde, em 1882, Ferdinand Lindemann mostrou que ele também é um número transcendente, ou seja, não pode ser raiz de nenhuma equação algébrica cujos coeficientes sejam racionais.
Cabe ressaltar que, de acordo com Maor (2008, p.251),
A descoberta dos números transcendentais não provocou o mesmo choque intelectual que os números irracionais tinham causado, dois mil e quinhentos anos antes, mas suas consequências foram igualmente significativas. Ela mostrou que, por trás da aparente simplicidade do sistema de números reais, oculta-se muitas sutilezas que não podem ser notadas simplesmente olhando-se a expressão decimal de um número. Mas a maior surpresa ainda estava por vir. Em 1874 o matemático alemão George Cantor (1845-1918) fez a espantosa descoberta de que existem mais números irracionais, e mais números transcendentais do que algébricos. Em outras palavras, longe de serem excentricidades, a maioria dos números reais é irracional e, entre os números irracionais, a maioria é transcendental!
O número de ouro é também conhecido como número áureo, segmento áureo, secção áurea.
Segundo Contador (2008, p. 393) “Esta é uma proporção geométrica única que contém dois termos; historicamente ela foi chamada pelos antigos de proporção áurea”, “e esta proporção só é possível quando o termo menor está para o termo maior, assim como o termo maior está para o todo”.
Contador (2008, p. 395) afirma que o número de ouro
[...] é constante e irracional, ele é conhecido como número de ouro ou número áureo, número porque é um desenvolvimento matemático e, porque calcula-se esse número; áureo porque é através dele que podemos construir coisas agradáveis à nossa vista, e com estética. A partir do século XX o matemático americano Mark Barr (1899) passou a usar a letra grega phi ϕ, a primeira letra do nome de Fídias ou Phídias, o grande e talentoso escultor grego que viveu por volta de 490 a.C. a 430 a.C., sabe-se que Fídia tinha conhecimento do número áureo e o utilizou em inúmeras obras de sua autoria. Ele é encontrado na Matemática dos povos antigos como egípcios, babilônicos, maias e astecas. A razão ou secção áurea tornou-se no decorrer do tempo a razão mais conhecida entre os matemáticos, perdendo apenas para a razão que estabelece π; que já era conhecida pelos gregos antes de Euclides, que a cita em Os Elementos, no livro VI, proposição 30.
Uma proporção divide um segmento de reta em média e extrema razão, quando o mais longo dos segmentos é a média geométrica entre o menor e o segmento todo, sendo b o segmento áureo.
Contador (2008, p. 395) explica que

O Homem Vitruviano, de Leonardo da Vinci, a Catedral de Notre-Dame (França), o Templo das Virgens ou o Parthenon (Grécia) e muitos outros, foram construídos usando a proporção áurea.
A origem do número e continua obscura, porém indícios de sua existência surgem no início do século XVII (época que John Napier inventou os logaritmos). Parece provável que tenha aparecido em uma fórmula do juro composto, pois o período citado foi marcado pela expansão do comércio multinacional e o grande número de transações financeiras.
Maor (2008, p. 241) diz que:
A história de π recua até uma época ancestral, já a história de e cobre apenas quatro séculos. O número π originou-se de um problema de geometria: como encontrar a circunferência e a área de um círculo. As origens de e não são tão claras, elas parecem recuar ao século XVI, quando se percebeu que a expressão (1+1/n)n, que aparecia na fórmula dos juros compostos, tendia a um certo limite – cerca de 2,71828 - à medida que n aumenta. Assim tornou-se o primeiro número a ser definido por um processo de limite, e=lim (1+1/n)n conforme n®∞.
Em 1873 Hermite demonstrou que e era um número transcendente (EVES, 2004).
Após pesquisa nos livros de história da matemática, foram analisados alguns exemplares de livros utilizados na Educação Básica, tanto livros do aluno quanto manuais do professor, para verificar como os números irracionais são apresentados, já que, conforme as Diretrizes Curriculares da Educação Básica, os alunos deverão reconhecer e realizar operações com números irracionais em diferentes conjunturas e reconhecer o número π como um irracional especial. Os livros utilizados na pesquisa compõem o PNLD 2011 até o PNLD 2017.
Em Sousa e Pataro (2012, 2013), Dante (2012), Bianchinni (2011) e Andrini e Vasconcellos (2012), nota-se um enfoque maior na descoberta dos irracionais pelos pitagóricos, com informações análogas às apresentadas na seção 3.
Em seus estudos, os discípulos de Pitágoras notaram que a medida da diagonal de um quadrado, cujo lado mede uma unidade, não poderia ser representada por um valor racional, isto é, não há inteiros a e b que possam ser escritos na forma 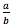 para emblemar essa medida (SOUSA e PATARO, 2012). Dante (2012) afirma que os babilônios tinham conhecimento do valor de
para emblemar essa medida (SOUSA e PATARO, 2012). Dante (2012) afirma que os babilônios tinham conhecimento do valor de 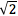 mas, diferente dos pitagóricos, não se preocuparam se tal número era ou não racional. Já os pitagóricos deram maior importância ao descobrir que tal valor que não apresentava nenhum padrão em sua infinita cadeia de casas decimais e isso causou um grande desequilíbrio religioso e filosófico, dado que, para eles tudo era número racional.
mas, diferente dos pitagóricos, não se preocuparam se tal número era ou não racional. Já os pitagóricos deram maior importância ao descobrir que tal valor que não apresentava nenhum padrão em sua infinita cadeia de casas decimais e isso causou um grande desequilíbrio religioso e filosófico, dado que, para eles tudo era número racional.
Apesar de não se ter certeza sobre a descoberta dos números irracionais, Bianchini (2011) apresenta o filósofo grego Aristóteles (384-322 a.C.) como sendo o autor da prova mais antiga da irracionalidade da diagonal do quadrado em relação ao seu lado. Os gregos clássicos relutaram em acatar a ideia, pois os números naturais e suas razões formavam a essência de todas as coisas (BIANCHINI, 2011).
Andrini e Vasconcellos (2012, p. 28) fazem um relato que vai ao encontro do comentado na seção 3:
Os matemáticos gregos antigos acreditavam que todos os problemas podiam ser resolvidos pelos números inteiros, pelos números racionais, suas operações e propriedades. No entanto, por volta de 400 a.C., eles descobriram, em problemas geométricos, números que não eram inteiros e que também não podiam ser escritos como quociente em números inteiros. Isso os abalou muito –que tipo de números seriam aqueles? A descoberta desses números, que eles chamaram de “inexprimíveis” e hoje chamamos de irracionais, provocou uma crise nos fundamentos da Matemática. Acredita-se que a descoberta dos irracionais tenha sido mantida em segredo durante certo tempo, enquanto os matemáticos tentavam entendê-los melhor.
Os outros exemplares apresentam somente uma breve explicação sobre a descoberta do número π e do número de ouro sem mencionar informações significativas sobre o conjunto dos irracionais, conforme os trechos a seguir.
Mori e Onaga (2012, p. 36) dizem que

Ainda,

Centurión e Jakubovic (2012) e Leonardo (2010) apresentam o tema de forma lúdica com algumas atividades em grupo com pouco enfoque histórico/teórico (apenas para manter uma conexão com o que estava sendo colocado em prática).
Comparando o conteúdo dos livros de história da matemática com os livros didáticos analisados, em relação aos livros didáticos, há tanto uma lacuna histórica quanto teórica na discussão sobre irracionais. Tomando Eves (2004) como um exemplo, ele apresenta uma abordagem histórica e teórica bem fundamentada, mostrando que ambas devem ser explanadas juntas, pois uma é a complementação da outra, isso faz com que quem esteja lendo entenda o conceito mesmo que não seja da área.
Os livros didáticos trazem o assunto em um texto mais sucinto, grande parte acaba por apresentá-lo em uma seção à parte do resto do conteúdo, apenas como curiosidade sobre a história da matemática. Talvez seja essa a raiz do problema que Santos (2007), Silva e Penteado (2009) e Broetto (2013) relatam, os alunos não compreendem os irracionais porque recebem um conteúdo sinótico no material didático e o professor acaba não tendo nenhum material de apoio para lecionar e auxiliar a compreensão dos alunos.
No Ensino Médio, segundo as Diretrizes, os assuntos abordados devem complementar de forma articulada os conteúdos já ministrados no Ensino Fundamental por meio da intercomunicação dos Conteúdos Estruturantes (PARANÁ, 2008). No Ensino Médio, Números e Álgebra são ministrados no primeiro ano.
Iezzi (2010, 2013) e Smole e Diniz (2010) trazem os irracionais de uma forma mais parecida com os livros didáticos do 8º ano. Dos livros consultados, apenas Ribeiro (2010) apresenta um conteúdo com teoria e história incorporadas uma a outra, além de citar autores que foram vistos durante a pesquisa somente nos livros de história da matemática, como Lambert por exemplo.
O suíço alemão Johann Heinrich Lambert (1728 – 1777) apresentou, em 1967, a primeira prova mostrando que π é um número irracional (RIBEIRO, 2010, p.30).
No manual do professor, há ainda uma complementação para que o docente possa enfatizar o método que Arquimedes utilizou para chegar até o valor aproximado de π, utilizando o método dos polígonos regulares.

Com esse estudo foi possível conhecer a trajetória histórica dos irracionais, compreendendo os conflitos que existiram durante a descoberta destes números.
O surgimento ocorreu com a necessidade de se calcular a diagonal de um quadrado de lado 1, que mede √2, sendo atribuída ao pitagórico Hipasus de Metapontum a descoberta, fato que custou a sua vida.
Na época, tal descoberta causou grande crise nos fundamentos da matemática, pois o único mecanismo para encontrar os valores das raízes quadradas envolvia os números quadrados e no caso da √2 não existe um número que elevado ao quadrado resultasse em 2.
Quando os Pitagóricos chegaram à conclusão que havia números que não podiam ser expressos pelo quociente de dois números inteiros, chamaram estes de alogon, que hoje traduzimos como irracionais, tendo na época duplo sentido, significando também “não deve ser falado”.
Séculos mais tarde, o matemático alemão George Cantor (1845-1918) provou que a maioria dos números reais é irracional.
Durante a pesquisa foram encontrados vários números irracionais, entre eles, destaco os mais conhecidos da história da matemática. É o caso do número π, razão áurea e o número e.
O número π é a razão entre o comprimento de uma circunferência e seu diâmetro. A razão áurea é obtida ao considerar que um termo menor está para o termo maior, assim como o termo maior está para o todo, permitindo construir “coisas” agradáveis a nossa vista, como O Homem Vitruviano, a Catedral de Notre-Dame e o Templo das Virgens ou o Parthenon. Por fim, o número e aparece na fórmula do juro composto, sendo o primeiro número a ser dado por um limite.
Nos livros didáticos em que os irracionais são apresentados historicamente são dadas informações a respeito da época em que foram descobertos, os responsáveis por tais desenvolvimentos, apresentando os irracionais “famosos” para relacioná-los com a história, enfatizando ao aluno a época em que foram descobertos, coincidindo com informações encontradas nos livros de história da matemática.
ANDRINI, A.; VASCONCELLOS, M. J. Praticando Matemática. (2012) 3. ed. São Paulo: Editora do Brasil, 8 v.
BERLINGHOFF, W.; GOUVÊA, F. Q. A Matemática através dos tempos. (2008) 2 ed. São Paulo: Blücher.
BIANCHINI, E. Matemática. (2011). 7. ed. São Paulo: Moderna. 4 v.
BOYER, C. B. História da Matemática. (1996) São Paulo: Edgard Blücher.
BRASIL. Secretaria de Educação Fundamental. Parâmetros curriculares nacionais: matemática. (1997). Brasília: MEC/SEF.
BROETTO, G. C. O ensino dos números irracionais na formação do professor de Matemática. In: ENCONTRO BRASILEIRO DE ESTUDANTES DE PÓS-GRADUAÇÃO EM EDUCAÇÃO MATEMÁTICA. 17., 2013, Vitória. Anais do XVII EBRAPEM. p. 1-12.
CAJORI, F. Uma história da Matemática. (2007). Rio de Janeiro: Ciência Moderna.
CENTURIÓN, M.; JAKUBOVIC, J. Matemática nos dias de hoje, 8º ano: na medida certa. (2015). São Paulo: Leya.
CENTURIÓN, M.; JAKUBOVIC, J. Matemática: Teoria e contexto. (2012). São Paulo: Saraiva. (Manual do professor).
CONTADOR, P. R. M. Matemática: uma breve história. (2008). 2.ed. São Paulo: Ed. Livraria da Física.
DANTE, L. R. Projeto Teláris: Matemática. (2012). São Paulo: Ática.
EVES, H. Introdução à história da matemática. (2004). Campinas: Editora da UNICAMP.
GARBI, G. A Rainha das Ciências. (2006). São Paulo: Ed. Livraria da Física.
IEZZI, G. Matemática: Ciência e Aplicações. (2010). 6. ed. São Paulo: Saraiva.
IEZZI, G. et al. Matemática: Ciência e aplicações. (2013). 7 .ed. São Paulo: Saraiva. v. 1.
LEONARDO, F. M. Projeto Araribá: matemática/organizadora. (2010). 3. ed. São Paulo: Moderna. (Obra coletiva, concebida e desenvolvida pela Editora Moderna.).
MAOR, E. e: A história de um número. (2008). 4. ed. Rio de Janeiro: Record.
MLODINOW, L. A Janela de Euclides: a história da geometria: das linhas paralelas ao hiperespaço. (2010). Tradução de Enézio E. de Almeida Filho. São Paulo: Geração Editorial.
MORI, I.; ONAGA, D. S. Matemática: ideias e desafios. (2012). 17. ed. São Paulo: Saraiva. (Manual do professor).
PADUA, E. M. M. Metodologia da pesquisa: abordagem teórico-prática. (2004). 10. Ed. rev. e atual. Campinas, SP: Papirus. (Coleção Magistério: Formação e Trabalho Pedagógico).
PARANÁ. Secretaria de Estado da Educação do Paraná. Diretrizes Curriculares da Educação Básica. (2008). Matemática. Disponível em: http://www.educadores.diaadia.pr.gov.br/arquivos/File/diretrizes/dce_mat.pdf Acesso em: 04 ago. 2017.
PASQUINI, R. C. G.; PEREIRA, A. C. C. Números reais e história da matemática: uma discussão acerca de abordagens nos livros didáticos. (2010) In. ENCONTRO NACIONAL DE EDUCAÇÃO MATEMATICA, 10., Salvador. Anais do V Encontro Nacional de Educação Matemática. p. 1-5.
REIS, L. G. Produção de monografias: da teoria à pratica. (2008). 2. Ed. Brasília: SENAC.
RIBEIRO, J. Matemática: Ciência, linguagem e tecnologia, 1: ensino médio. (2010) São Paulo: Scipione.
ROQUE, T. História da matemática: uma visão crítica, desfazendo mitos e lendas. (2012). Rio de Janeiro: Zahar.
SANTOS, J. C. Números Reais: Um desafio na Educação Básica. (2007). Monografia (Curso de especialização em Matemática para professores do Ensino Fundamental e Médio) – Universidade Federal Fluminense, Niterói.
SANTOS, M. V. F. Complexos e polinômios. (2014). X ao Cubo.
SILVA, B. A.; PENTEADO, C. B. Fundamentos dos números reais: Concepções de professores e viabilidade de início de estudo da densidade no ensino médio. (2009). Educ. Matem. Pesq., São Paulo, v. 11, n. 2, p. 351-371.
SMOLE, K. C. S.; DINIZ, M. I. S. V. Matemática: ensino médio. (2010). 6. ed. São Paulo: Saraiva.
SOUZA, J. R.; PATARO, P. R. M. Vontade de saber matemática. (2012). 2. ed. São Paulo: FTD.
1. Aluno do curso de Licenciatura em Matemática da Universidade Estadual do Centro-Oeste (UNICENTRO). alcidestkz@gmail.com
2. Professora do Departamento de Matemática da Universidade Estadual do Centro-Oeste (UNICENTRO). kbarone@unicentro.br