ISSN 0798 1015
ISSN 0798 1015
Vol. 40 (Nº 5) Año 2019. Pág. 25
VIDES, Saúl E. 1; RIVERA, Jhonny A. 2; HERNANDEZ, Carlos G. 3
Recibido: 17/10/2018 • Aprobado: 27/01/2019 • Publicado 11/02/2019
RESUMEN: Este artículo hace referencia del uso de la ingeniería didáctica para el proceso de enseñanza de la distribución de Poisson. Para su desarrollo es implementada en la institución de educación superior Universidad Popular del Cesar ubicada en Valledupar – Colombia. Los resultados evidencian que la implementación de la ingeniería didáctica permite que el alumno se apropie del objeto matemático distribución de poisson, convirtiéndose en un instrumento metodológico para la enseñanza y para la investigación, que brinda la posibilidad de desarrollar una acción racional sobre un objeto de aprendizaje, puesto que se intenta captar la complejidad del proceso de enseñanza en situación escolar. Esta se compone de cuatro fases: Análisis preliminar, Diseño de una situación didáctica y su análisis a priori, Experimentación, Análisis a posteriori y validación; apoyada en la teoría de las situaciones didácticas. |
ABSTRACT: This article refers to the use of didactic engineering for the process of teaching the Poisson distribution. For its development it is implemented in the higher education institution Universidad Popular del Cesar located in Valledupar - Colombia. The results show that the implementation of didactic engineering allows the student to appropriate the mathematical object poisson distribution, becoming a methodological instrument for teaching and for research, which provides the possibility of developing a rational action on a learning object, since it tries to capture the complexity of the teaching process in school situation. This consists of four phases: Preliminary analysis, Design of a didactic situation and its a priori analysis, Experimentation, A posteriori analysis and validation; supported by the theory of didactic situations. |
La estadística como ciencia, está en notable crecimiento; sin embargo, la Didáctica de la Estadística tiene una evolución incipiente. El número de investigaciones sobre la enseñanza de esta es aún escaso y, sólo se están comenzando a conocer las dificultades de aprendizaje de los estudiantes en los conceptos más importantes de esta disciplina (Batanero, 2001).
La ingeniería didáctica surgió como metodología de investigación dentro de la Didáctica de las Matemáticas en Francia en 1980. La misma es una forma de trabajo didáctico que se basa en los conocimientos científicos de su dominio y se somete a un control de tipo científico.
Como metodología de investigación, la ingeniería didáctica se caracteriza en primer lugar por un esquema experimental basado en las “realizaciones didácticas” en clase, es decir, sobre la concepción, realización, observación y análisis de secuencias de enseñanza.
Se propone una experiencia educativa (Secuencia didáctica) conducida por el marco de la ingeniería didáctica y desarrollada con alumnos de ingeniería, con el fin de documentar y analizar las formas en que abordan, piensan, argumentan, negocian y discuten cuando deben tratar con sus conocimientos y con las expectativas metamatemáticas propias de los participantes. En ambos casos hay interés, sobremanera, en entender cómo construyen su conocimiento.
El producto obtenido de esta investigación en el campo de la Estadística tiene como objetivo incidir positivamente en el proceso enseñanza de la distribución de Poisson a través de un sistema didáctico formado por: el alumno, el profesor y el conocimiento a enseñar a través de una secuencia didáctica donde el alumno pueda transitar por situaciones problema, que le den la oportunidad de vivir y cuestionar el objeto matemático, y a la vez implementarlo en forma regular en la enseñanza de la estadística a nivel universitario.
A l vez esta propuesta admite la siguiente pregunta:
¿El uso de la ingeniería didáctica permite la enseñanza de la distribución de Poisson a través de la ingeniería didáctica?
Enseñar la distribución de Poisson a través de la ingeniería didáctica.
• Describir las componentes epistémicas, didácticas y cognitivas del concepto de la distribución de Poisson.
• Construir una situación didáctica de la enseñanza de la distribución de Poisson, para los alumnos de ingeniería.
• Validar la implementación de la situación didáctica en la enseñanza de la distribución de Poisson.
• Elaborar un modelo didáctico para la enseñanza de la distribución de Poisson en el contexto.
Esta se soporta en el carácter específico del conocimiento matemático y en la importancia particular de las situaciones de enseñanza, la gestión de las mismas y los procesos cognitivos tanto de los alumnos como del profesor. Una situación didáctica se establece entre un grupo de alumnos y un profesor, quien usa un medio didáctico donde se incluyen los problemas, materiales e instrumentos, con el fin específico de ayudar a sus alumnos a reconstruir un cierto conocimiento.
Para lograr el aprendizaje, el alumno debe interesarse personalmente por la resolución del problema planteado en la situación didáctica. De acuerdo con Brousseau, creador de la teoría, el trabajo intelectual del alumno debe ser en ciertos momentos comparable al de los propios matemáticos, en donde este debe tener oportunidad de investigar sobre problemas a su alcance, formular, probar, construir modelos, lenguajes, conceptos, teorías, intercambiar sus ideas con otros, reconocer las que son conformes con la cultura matemática, adoptar las ideas que le sean útiles.
Dentro del ámbito de la enseñanza de los saberes matemáticos, Brousseau distingue para una situación didáctica determinada: un estado inicial y el conjunto de diversos estados posibles. Se explicitan las reglas que permiten pasar de un estado a otro (componente estructural). Según sean las relaciones se definen situaciones de:
-Acción, corresponde a la interacción entre alumnos y el medio físico. El esquema de la dialéctica de la acción pertenece a una de toma de decisión del alumno para organizar la actividad que enriquezca el modelo para resolver problemas.
-Formulación, cuyo objetivo es la comunicación de informaciones, entre alumnos, a través de la dialéctica.
-Validación, en la que se trata de convencer a uno o varios interlocutores de la validez de las afirmaciones que se hacen.
-Institucionalización, destinada a establecer convenciones sociales (Gálvez, 1994).
Esas situaciones conjugan una dialéctica global que las incluye a todas. En general la dialéctica presente en situaciones de acción, sistematiza la interacción efectiva sobre el medio por el sujeto que construye el saber; la misma necesita condiciones pertinentes que le motiven a acciones e informaciones accesibles. Esta, consecuentemente, tiene un caso particular en la dialéctica de la formulación; esta última es producto de las relaciones dadas por el cambio de información con otros sujetos que dan paso a la creación de un lenguaje y a la aparición de un saber. De igual modo, la dialéctica de validación constituye un caso particular de la situación anterior; cuando sobre los cambios de información se toman decisiones produciéndose pruebas para demostrar las afirmaciones. Por último, se tiene el término institucionalización, aparecido en la Escuela de Verano de Didáctica en 1980; la misma corresponde a los saberes reconocidos (legitimados) son convencionalismos y explican el status cognitivo de un conocimiento o saber, (Escalona, 2001).
Creada por Chevallard (1995), para quien el conocimiento generado por la élite de matemáticos, no llega al aula tal y como es producido, sino que sufre un proceso que ha denominado transposición didáctica. Siguiendo sus ideas, el “saber erudito” pasa a ser un “saber a enseñar”, luego de ser validado por una “nooesfera” que le confiere el status de conocimiento a ser abordado en la escuela. No se trata de una elementarización burda del conocimiento, ni de una mera simplificación del mismo, sino por el contrario, el producto de los ajustes didácticos los cuales permiten una presentación ajustada del conocimiento de origen.
La transposición didáctica no es caprichosa ni voluntaria, sino producto de las restricciones que la sociedad impone a las prácticas educativas (Cantoral, 1995). La primera etapa de este proceso se produce cuando el científico pone a consideración de sus pares los resultados obtenidos en su investigación. Esto le exige hacerlo público, es decir, quitarle su sello personal, transformarlo en un saber a ser “comunicado”, para lo cual debe dejarlo libre de los resabios de su creación, es decir, de sus errores, de sus caminos truncados, de sus retrocesos, para volverlo un saber cultural, por tanto, despersonalizado, descontextualizado y atemporal, esto es, que pueda vivir en cualquier momento. Aparece así, lo que Chevallard ha dado en llamar el “saber sabio o erudito”. Luego, cuando este saber público entra en la escuela a través del profesor, comienza un proceso de re‐personalización, re‐contextualización y temporalidad de los conocimientos, es decir, se le debe dotar de intencionalidad, de una nueva naturaleza, de otro sentido y escenario en el cual ser entendido, interpretado y validado por los alumnos.
Un modo de realizar la transposición didáctica es el enfoque socioepistemológico. Este proceso estudia el entendimiento de la construcción del conocimiento matemático de acuerdo con lo que organizan los grupos humanos normado por lo institucional y cultural. Se trata de entender tal constitución para hacer que el conocimiento sea funcional, se integre al humano para transformar el mundo, su naturaleza y por lo tanto a él. Para responder a tal conocimiento se debe hacer estudios sobre su uso en situaciones específicas donde se resignifique el conocimiento matemático en cual se debate entre su funcionamiento y forma (Cordero, 2003, 2005, 2006a, 2006b).
Este enfoque modela la construcción social del saber matemático; aquí el saber resulta funcional en las dimensiones cognitiva, didáctica, epistemológica y social. La práctica social es la que genera el conocimiento, teniendo en cuenta el papel que los escenarios históricos, culturales e institucionales desempeñan en la actividad humana al momento de producir un conocimiento. Para este el conocimiento es relativo al contexto y a la situación.
Las aproximaciones epistemológicas tradicionales asumen el conocimiento como el resultado de la adaptación de las explicaciones teóricas con las evidencias empíricas, ignorando el papel que los escenarios históricos, culturales e institucionales desempeñan en toda actividad humana. La Socioepistemología se plantea el examen del conocimiento situado, aquel que atiende a las circunstancias y escenarios socioculturales particulares. El conocimiento, en este caso, se asume como el fruto de la interacción entre la epistemología y los diversos factores sociales. Su núcleo es la práctica social, es decir, la actividad matemática, no está separada del sistema cultural.
Según esta perspectiva el proceso de aprendizaje consiste en interacciones entre concepciones operacionales y estructurales. La primera abarca nociones matemáticas como procesos, algoritmos y acciones y, significan los primeros pasos para la adquisición de nuevos conceptos; las concepciones estructurales entienden los conceptos matemáticos como objetos abstractos. En la conformación de nuevos conceptos se distingue tres fases o estructuración progresiva: Interiorización, condensación y reificación (Santos-Matamoros, Gloria; García, Mercedes y LLinares, Salvador ; 2008). Estos procesos pueden iniciarse donde culmina un ciclo de los mismos, una cosificación puede ser el inicio de una interiorización de nivel superior (Escalona, María. 2001: 51-52).
El tipo de metodología empleada en esta investigación es descriptiva, correlacional y explicativa; porque a través de esta, se pretende reseñar con precisión como los alumnos conforman el concepto distribución de Poisson. El diseño de esta indagación es de campo no experimental y se fundamenta a partir de teorías didácticas de las matemáticas como las de Brousseau (1981) y para la realización del análisis y descripción de los hechos, se procede atendiendo las fases de la ingeniería didáctica.
De acuerdo con Artigue (1995), el término ingeniería didáctica designa un conjunto de secuencias de clase concebidas, organizadas y articuladas en el tiempo de forma coherente por un profesor-ingeniero para efectuar un proyecto de aprendizaje de un contenido matemático dado para un grupo de estudiantes. A lo largo de los intercambios entre el profesor y los participantes, la investigación evoluciona bajo las reacciones de los alumnos en función de las decisiones y elecciones del profesor. Así, la ingeniería didáctica es, al mismo tiempo, un producto, resultante de un análisis a priori, y un proceso, resultante de una adaptación de la puesta en funcionamiento de un producto acorde con las condiciones dinámicas de una clase. Por tanto, se destaca la intencionalidad por lograr un objetivo de enseñanza previamente establecido y esto se logra a través del conjunto de relaciones establecidas entre los alumnos, un cierto medio (instrumentos u objetos) y el docente con el fin de conseguir que los participantes se apropien de un saber constituido en vía de constitución y finalmente institucionalizarlo.
De acuerdo con Artigue (1995), las fases de la ingeniería didáctica aplicada en esta investigación son:
Análisis Preliminares: Se refiere a los conocimientos teóricos didácticos generales y específicos del campo de estudio y al análisis de: la epistemología de los contenidos a enseñar, la enseñanza tradicional y sus efectos, las concepciones de los alumnos, las dificultades y obstáculos que se presentan en el aprendizaje, el desarrollo científico en la sociedad de la época, las condiciones bajo las cuales se presentará la situación didáctica efectiva y los objetivos de la investigación, entre otros. A continuación, se muestra una descripción de las tres dimensiones de esta fase:
En esta investigación, la epistemología se utiliza como reflexión sobre la esencia del concepto estadístico distribución de Poisson, los procesos y condiciones que ha provocado su desarrollo, las características de la actividad estadística tanto futura, como presente y pasada. Y todo lo que constituye la naturaleza específica de un dominio matemático u otro (Artigue, 1995).
El uso de la epistemología ayuda a mantener una visión extrínseca de los objetos enseñados (devolviendo una historicidad tanto a estos objetos, porque la enseñanza tradicional tiende a presentarlos como objetos universales). El análisis epistemológico ayuda a la Didáctica a desprenderse de la ilusión de transparencia de los objetos que maneja a nivel de saber y ayuda al profesor a librarse de las representaciones epistemológicas erróneas que tiende a inducir su práctica de enseñante.
Se promueve la construcción del conocimiento sobre la distribución de Poisson. Se diseña una secuencia didáctica que se adapta a la perspectiva institucional, y distingue dos tipos fundamentales de relaciones con el objeto a aprender: las relaciones personales de los alumnos y también las relaciones institucionales que condicionan estas relaciones personales y su evolución. En esta se considera la teoría sobre Situaciones Didácticas.
Esta dimensión tiene en cuenta las concepciones de los alumnos, sus dificultades y los obstáculos a los cuales deben enfrentar para apropiarse del objeto matemático distribución de Poisson, puestas en juego por la secuencia implementada. Para su reflexión se tienen las conformaciones del concepto distribución de Poisson; así como las representaciones que los participantes tengan sobre el mencionado concepto:
Diseño y análisis a priori de las situaciones de la ingeniería didáctica: Se analiza qué podría aprender en esta situación el alumno en función de las posibilidades de acción, decisión, control y validación de las que dispone, una vez puesta en práctica, cuando trabaja independientemente del profesor.
Se prevén los comportamientos posibles y se trata de demostrar cómo el análisis realizado permite controlar su significado y asegurar, que, si se producen los comportamientos esperados, sean resultado de la puesta en práctica del conocimiento pretendido por el aprendizaje.
Experimentación: En esta etapa se ejecuta la situación didáctica diseñada; es decir, se implementa en condiciones controladas. Los medios para reproducir los sucesos que se intenten desarrollar, para su posterior análisis quedan bajo la responsabilidad y elección del investigador. Es importante el control de las actividades y el registro de los sucesos, para que el conocimiento y caracterización de los mismos produzcan la calidad y fidelidad de la siguiente etapa.
Análisis a posteriori y evaluación: Se basa en el conjunto de datos recogidos durante la experimentación. El análisis se fundamenta en un análisis de los datos obtenidos en la implementación, para la confrontación con el análisis a priori.
Participaron en la experiencia 20 alumnos (5 mujeres y 15 hombres) con edades entre 18 y 20 años, pertenecientes a los diferentes programas de ingenierías, de los cuales todos habían cursado la asignatura estadística, que es la asignatura en donde se tratan los contenidos relacionados con la distribución de Poisson.
Para el desarrollo de esta investigación, se implementó una situación didáctica diseñada por los investigadores, donde se planteaban preguntas y problemas relacionados con el objeto matemático distribución de poisson. Constó de ocho preguntas y en donde se les solicitó interpretar la mayoría de los resultados a los que finalmente deberían llegar.
En esta investigación se exploraron los significados y las concepciones que los alumnos tienen respecto al objeto matemático distribución de Poisson, para identificar situaciones que no favorecen la construcción de este. El análisis de los resultados pasó por las siguientes etapas:
Identificación del nivel de interpretación de la variable aleatoria
Observación del nivel de interpretación de la distribución de Poisson
Indagar como es que los alumnos vinculan el significado de la variable aleatoria con el de la distribución de Poisson.
Lo anterior condujo al conocimiento de los elementos que conllevan a los alumnos a utilizar incorrectamente la distribución de Poisson.
Los resultados que arrojaron esta investigación son los siguientes:
La situación didáctica fue resuelta individualmente y se debió utilizar calculadora; el tiempo de duración para el desarrollo de la situación didáctica se estableció de 2 horas.
Generalmente se dice que la distribución de Poisson tiene su mayor aplicación, cuando en el experimento que se realiza ocurren sucesos llamados raros, los cuales se identifican con una probabilidad de éxito sumamente pequeña p y el número de observaciones n grande.
Esta distribución halla la probabilidad de ocurrencia de cualquier número de éxitos x por unidad de medición (minuto, hora, día, centímetro, metro, etc.), y en estos problemas para su solución dan el valor del parámetro lambda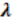 
; o sea, el promedio o razón de ocurrencia del evento aleatorio por unidad de tiempo o espacio y el número de éxitos. Donde 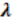=np, y para calcular la probabilidad se utiliza la fórmula:
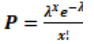
Con base a la información dada resolver:
1. Durante un experimento de laboratorio el número promedio de partículas radiactivas que pasan a través de un contador en un milisegundo es cuatro. ¿Cuál es la probabilidad de que seis partículas entren al contador en un milisegundo?
2. La producción de televisores en una fábrica trae asociada una probabilidad de defecto del 2%, si se toma un lote o muestra de 85 televisores, obtener la probabilidad de que existan 4 televisores con defectos.
3. Si el 2% de las bombillas fabricadas por una compañía son defectuosas, hallar la probabilidad de que, en una muestra de 100 bombillas, 5 sean defectuosas.
4. Una compañía telefónica recibe llamadas a razón de 4 por minuto.Calcular la probabilidad de:
(a) Recibir 2 llamadas en un minuto (b) No recibir ninguna llamada en un minuto.
(c) Recibir menos de 3 llamadas en un minuto (d) Recibir más de 3 llamadas en un minuto.
5. Si el 2% de los libros encuadernados en cierto taller tiene encuadernación defectuosa, para obtener la probabilidad de que 5 de 400 libros encuadernados en este taller tengan encuadernaciones defectuosas usamos la distribución de Poisson.
6. Camiones llegan a una empresa de transporte con un tiempo medio entre llegadas de 5 minutos. ¿Cuál es la probabilidad de que no llegue ningún camión durante un intervalo de treinta minutos?
7. Consideremos la distribución de Poisson para µ = 64. ¿Cuál es la probabilidad de obtener 72 sucesos?
8. Supóngase que estamos investigando la seguridad de un crucero muy peligroso. Los archivos de la policía indican una media de cinco accidentes por mes en él. El número de accidentes está distribuido conforme a la distribución de Poisson, y la división de seguridad en carreteras quiere calcular la probabilidad de exactamente 0, 1, 2,3 y 4 accidentes en un mes determinado.
Los resultados arrojados por esta investigación reflejan en los alumnos los siguientes aspectos: Poco reconocimiento de la definición de factorial de un número.
Dificultad para calcular el parámetro lambda (
Desconocimiento de los criterios para calcular la probabilidad de un evento aleatorio a través de la distribución de poisson, los cuales son:
Desconocimiento de que los éxitos buscados (valores de la variable x) en la distribución de poisson son expresados por unidad de área, tiempo, etc.
Esta investigación arrojó los siguientes resultados:
La epistemología del objeto matemático distribución de poisson contribuyó a un aprendizaje significativo de éste, ya que los alumnos reconocieron los procesos y condiciones que provocaron su desarrollo.
Los conceptos de probabilidad, variable aleatoria discreta, sumatoria, factorial asociados a la distribución de Poisson son reconocidos por pocos alumnos presentes en esta investigación.
Es necesario la construcción de secuencias didácticas para la mejor comprensión del concepto de la Distribución de Poisson.
Los alumnos necesitan más acompañamiento permanente para la enseñanza y aprendizaje de la distribución de Poisson.
Artigue, M. (1995). La enseñanza de los principios del cálculo: problemas epistemológicos, cognitivos y didácticos. En Artigue, M.; Douady, R.; Moreno, L. y Gómez, P. (editor). Ingeniería Didáctica en Educación Matemática. Una Empresa Docente. Bogotá. Grupo Editorial Iberoamérica.
Batanero Carmen (2001). Didáctica de la Estadística. Grupo de Educación Estadística. Universidad de Granada.
Brousseau Guy. (1981). “Problèmes de didactique des décimaux“. Recherches en Didactique des Mathématiques. Vol. 2, pp. 37-127. (1986). “Fondements et méthodes de la didactique des mathématiques“.
Cordero, Francisco (2003). Reconstrucción de significados del Cálculo Integral: La noción de acumulación como una argumentación. Grupo Editorial Iberoamérica. México.
Escalona, María (2001) Procesos cognitivos visuales y las intuiciones matemáticas y probabilísticas. Tesis doctoral inédita, mención publicación. Maracaibo, Doctorado en Ciencias Humanas, Facultad de Humanidades y Educación, Universidad del Zulia, 264 pp.
Estándares Básicos de Competencias en Matemáticas (1997). Disponible en: http://www.mineducacion.gov.co/1759/articles116042_archivo_pdf2.pdf
1. Universidad del Zulia, Maracaibo, Venezuela. Magíster en Matemática Aplicada. Docente Investigador Universidad Popular del Cesar. saulvides@unicesaredu.co
2. Universidad del Zulia, Maracaibo, Venezuela. Magíster en Matemática Aplicada. Docente Investigador Universidad Popular del Cesar. jhonnyrivera@unicesar.edu.co
3. Universidad Popular del Cesar, Valledupar, Colombia. Licenciado en Matemáticas y Física. Docente Investigador Universidad Popular del Cesar. carloshernandez@unicesar.edu.co