ISSN 0798 1015

Vol. 40 (Nº 29) Ano 2019. Pág. 19

Ensinando Matemática à Luz da Teoria de Edgar Morin: Uma Abordagem para o Ensino-Aprendizagem de Cálculo Diferencial e Integral I

Teaching Mathematics in the Light of Edgar Morin Theory: An Approach to Teaching-Learning Differencial and Integral Calculus I

HALLAL, Renato 1; PINHEIRO, Nilcéia A. M. 2; OLIVEIRA, Reginaldo 3 & FALCÃO, Adair P. 4

Recebido: 14/05/2019 • Aprovado: 04/08/2019 • Publicado 02/09/2019

Conteúdo

1. Introdução

2. Fundamentação Teórica

3. Metodologia

4. Desenvolvimento

5. Conclusão

Referências bibliográficas

1. Introdução

Participando diretamente do mundo acadêmico, nota-se que é cada vez maior o empenho do docente para ensinar seus alunos de maneira lúdica e prazerosa o conteúdo matemático, devido ao histórico de alunos terem dificuldade a entender essa disciplina.

As disciplinas de Matemática são consideradas pelos alunos, mesmo por aqueles que frequentam cursos da área de ciências exatas, como sendo as mais difíceis de suas grades curriculares e, como consequência desta dificuldade, são elas as que geram maiores índices de reprovação.

Em particular, nas universidades, a disciplina de CDI-I, proposta no primeiro semestre dos cursos tem sido a principal protagonista desses elevados índices de reprovações e evasões estudantis, sendo considerada pelos alunos uma disciplina com elevado grau de abstração. Além disto, pesquisas apontam que um dos fracassos dos acadêmicos na disciplina de CDI-I refere-se a forma rígida e inflexível em que a disciplina está organizada, bem como das práticas pedagógicas adotadas pelos professores (ZAPERLON, 2016, p. 14).

Dessa maneira, observa-se que o ensino da matemática tem enfrentado dificuldades no que diz respeito ao seu ensino e aprendizagem. Na literatura, podemos encontrar estudos que buscam entender as razões dessas dificuldades e, ao mesmo tempo, encontrar alternativas que possam contribuir para a aprendizagem dos conteúdos estudados nessas disciplinas (CURY, 2006; FERREIRA & BRUMATTI, 2009 e SILVA & FERREIRA, 2009). Mediante tal fato, sentimos a necessidade de uma “nova maneira” de interpretar e trabalhar os conteúdos propostos nesta disciplina, sem contudo, desconsiderar o grau de complexidade e os níveis de qualidade requeridos pela universidade.

Diante do exposto, pretende-se com este trabalho, apresentar uma proposta para o estudo de Cálculo Diferencial e Integral I, utilizando como pauta o conteúdo de limite. Nessa perspectiva, será apresentado uma sequência didática adaptada a teoria do conhecimento de Morin (2000), com a finalidade de facilitar a compreensão do conteúdo de limite presente na disciplina de Cálculo Diferencial e Integral I. Deste modo, como ponto de partida para os estudos, temos: Quais as contribuições que os Princípios de Conhecimento de Morin (2000) pode trazer aos processos de ensino e aprendizagem de Limite?

Nesta seção, serão abordados a biografia e uma breve teorização sobre os princípios do conhecimento pertinente de Edgar Morin.

2.1. Biografia de Edgar Morin

Edgar Morin nasceu em 1921 em Paris. Seu nome verdadeiro é Edgar Nahoum. Fez os estudos universitários de História, Geografia e Direito na Sorbonne. Ingressou no Centro Nacional de Pesquisa Científica (CNRS), onde realizou um dos primeiros estudos etnológicos produzidos na França, sobre uma comunidade da região da Bretanha. Criou o Centro de Estudos de Comunicações de Massa e as revistas Arguments e Comunication (MORIN, 2011).

Em 1968 começou a lecionar na Universidade de Nanterre. Passou um ano no Instituto Salk de Estudos Biológicos em La Jolla, na Califórnia, onde acompanhou descobertas da genética. Redigiu em 1994, com o semiólogo português Lima de Freitas e o físico romeno Basarab Nicolescu, um manifesto a favor da transdisciplinaridade (LIVRONAUTAS, 2018).

O início do século XX foi marcado por duas revoluções científicas: a teoria da relatividade de Albert Einstein (1858-1947) e a mecânica quântica de Max Planck (1879-1955). Ambas obrigaram a humanidade a rever doutrinas e tiveram aplicações nas mais diversas áreas, da filosofia à indústria bélica. Essas e outras reformulações do conhecimento humano levaram Morin a definir sete princípios, (a) os princípios sistêmico (o todo é mais do que a soma das partes), (b) hologramático (o todo está em cada parte), (c) do ciclo retroativo (a causa age sobre o efeito e vice-versa), (d) do ciclo recorrente (produtos também originam aquilo que os produz), (e) da auto-eco-organização (o homem se recria em trocas com o ambiente), (f) dialógico (associação de noções contraditórias) e (g) de reintrodução do conhecido em todo conhecimento (MORIN, 2011).

Entre suas principais obras literárias, destacam-se (a) os sete saberes necessários à educação do futuro, (b) o método, (c) o problema epistemológico da complexidade, (d) religando os saberes, entre outros.

Nosso trabalho é inspirado nas ideias de Morin, no livro Os Sete Saberes Necessários à Educação do Futuro, dando ênfase, especificamente ao Capítulo II – Os Princípios do Conhecimento Pertinente, apresentado na próxima seção.

2.2. Os Princípios do Conhecimento Pertinente

Em seu livro os sete saberes necessários à educação do futuro, em o Princípio do Conhecimento Pertinente, Morin (2000, p. 35) inicia o parágrafo com interrogações, ou seja [...] Como perceber e conceber o Contexto, o Global (a relação todo/partes), o Complexo? Para articular e organizar os conhecimentos e assim reconhecer e conhecer os problemas do mundo, é necessária a reforma do pensamento. Esta reforma é a questão fundamental da educação, já que se refere à nossa aptidão para organizar o conhecimento.

Morin (2000, p. 36) acrescenta,

Esse problema universal confronta-se a educação do futuro, pois existe inadequação cada vez mais ampla, profunda e grave entre, de um lado, os saberes desunidos, divididos, compartimentados e, de outro, as realidades ou problemas cada vez mais multidisciplinares, transversais, multidimensionais, transnacionais, globais e planetários.

Essas inadequações desconectam o contexto, o global e o complexo. Assim, para que o conhecimento seja pertinente, a educação deve torna-los evidentes/conectados.

Quanto ao contexto, o autor relata que [...] o conhecimento das informações de dados isolados é insuficiente, é necessário situar as informações e os dados em seu contexto para que adquiram sentido. Morin (2000, p. 37) acrescenta, “a contextualização é condição essencial da eficácia do funcionamento cognitivo”.

Quanto ao global, Morin faz relações entre o todo e as partes. O global é o conjunto das diversas partes ligadas a ele de modo organizacional (MORIN, 2000).

Morin (2000, p. 37) relata,

O todo tem qualidades ou propriedades que não são encontradas nas partes, se estas estiverem isoladas umas das outras, e certas qualidades ou propriedades das partes podem ser ocultadas pelas restrições provenientes do todo. Portanto é preciso recompor o todo.

Assim se tem a virtude cognitiva do princípio de Pascal, sobre a educação do futuro, o qual considera impossível [...] conhecer o todo sem conhecer particularmente as partes, tampouco conhecer as partes sem conhecer o todo (PASCAL, 1976).

Quanto ao complexo, Morin (2000, p. 38) diz que a complexidade é a união entre as unidades e a multiplicidade, elas devem ser tecidas juntas. Existe um tecido interdependente, interativo entre o objeto de conhecimento e seu contexto, as partes e o todo, o todo e as partes e as partes entre si. Deste modo, o conhecimento pertinente deve enfrentar essa complexidade, ou seja, essa diversidade.

Segundo Morin (2000, p. 39) para que promova essa teorização deve-se ativar a mente humana, permitindo assim, melhor desenvolvimento das competências especializadas. O conhecimento, ao buscar construir-se ao contexto, ao global e ao complexo deve mobilizar o que o conhecedor sabe sobre o assunto. Dessa maneira, há uma correlação entre a mobilização dos conhecimentos dos conjuntos e a ativação da inteligência geral.

A educação deve auxiliar a ativação da mente em formular e resolver problemas e, de forma correlata, estimular o uso da inteligência geral. Este uso é a busca pela curiosidade, se trata em estimular o que está adormecido, refere-se ao despertar.

Este trabalho iniciou-se no Programa de Pós-Graduação em Ensino de Ciência e Tecnologia na Universidade Tecnológica Federal do Paraná (UTFPR-PG) em aulas sobre o livro “os sete saberes necessários à educação do futuro”, na disciplina de Docência e Empreendedorismo. No decorrer das aulas, o professor e os alunos debatiam, fomentavam e davam exemplos sobre cada capítulo do livro estudado. Como atividade, cada aluno deveria desenvolver um trabalho que lhe fosse estimulante/interessante. Assim surgiu este artigo.

Desta maneira, para o andamento desta pesquisa, fizemos levantamentos bibliográficos, buscamos conversar com outras pessoas sobre o assunto e buscamos encontrar exemplos que estimulassem a compreensão do tema. Por este motivo, caracterizamos esta pesquisa como exploratória.

O objetivo, é apresentar uma sequência didática inspirado na teoria do conhecimento de Morin (2000), com a finalidade de facilitar a compreensão do conteúdo de limite presente na disciplina de Cálculo Diferencial e Integral I. Segundo Peretti & Costa (2013, p. 06) sequência didática é um termo usado na educação para definir um conjunto de atividades, encadeada de passos e ligadas entre si, para tornar mais eficiente o processo de aprendizado.

Neste trabalho, a sequência didática foi amoldada ao método de Dolz; Noverraz & Schneuwly (2004, p. 98), conforme ilustrado na Figura 1.

Figura 1
Esquema da sequência didática

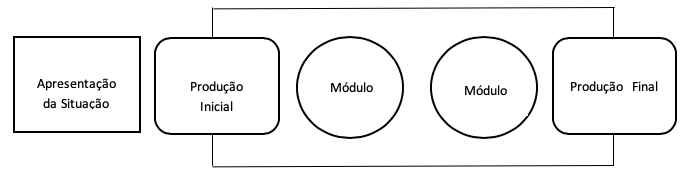
Fonte: DOLZ; NOVERRAZ & SCHNEUWLY, 2004, p. 98

Segundo este esquema, a Apresentação da Situação refere-se ao levantamento dos conhecimentos prévios dos alunos, a Produção Inicial refere-se ao conteúdo a ser trabalho, ao objetivo e a definição do público alvo, os Módulos referem-se as etapas para se conseguir alcançar os objetivos e, a Produção Final é o momento do aluno colocar em prática tudo que foi trabalhado em cada módulo.

Com base na Figura 1, na próxima seção, será apresentado o desenvolvimento da atividade proposta, focando principalmente, “o módulo”.

Para explanar o desenvolvimento, tem-se:

4.1. Etapa 1: Apresentação da Situação

Esta etapa tem como finalidade fazer uma busca sobre o conhecimento prévio dos alunos, bem como, prepara-los para o conteúdo que será trabalhado, limite. Para tanto, aconselha-se verificar o conhecimento dos alunos em relação ao Pré-Cálculo; como potenciação, fatoração, simplificação, produtos notáveis e funções.

Nesta seção, o objetivo é nivelar os alunos com os conhecimentos básicos da matemática, facilitando a ancoragem para se aprender o novo conteúdo. Levando para a teoria de Morin (2000), podemos dizer que, para assimilar o global, devemos aprender as partes para se chegar ao todo. Ao trabalhar cada conteúdo de Pré-Cálculo com os alunos, devemos também, fazer uma relação entre um conteúdo e outro, de modo a ativar a inteligência geral (ou seja, despertar a curiosidade no aluno). Nesta etapa a interação aluno/professor deve ser intensa.

4.2. Etapa 2: Produção Inicial

Nesta etapa, o propósito é fazer uma apresentação sobre o novo conteúdo, destacando o que será trabalhado, como será trabalhado, qual o objetivo dos estudos, entre outras questões. Como ideia inicial, buscamos organizar estes dados na Tabela 1.

Tabela 1
Apresentação do conteúdo a ser trabalhado.

Fonte: Elaborado pelo autor

Após expor como será trabalhado os conteúdos, entramos na etapa “módulo”, ponto chave deste trabalho.

4.3. Etapa 3: Módulo

A partir de agora, estudaremos “LIMITE”. Veremos que em Cálculo, o limite nos permite verificar qual o comportamento dos valores da função f(x) , quando  está próximo de um ponto . No módulo 1 abordaremos uma noção intuitiva para os estudos de limite, bem como, uma prévia de como calcular limite.

Para tanto, neste módulo, buscamos facilitar a aprendizagem fazendo uma analogia ao que propõe Morin (2000), ou seja:

A - Contextualizamos o conceito de limite, fazendo uma relação com a fogueira (trabalhamos o contexto);

B - Resolvemos o limite de uma função buscando entender as partes, para se entender o todo, ou seja, mostramos que para se resolver limite existe a necessidade de se entender o desenvolvimento de outros conceitos matemáticos, como função, potencialização, produtos notáveis, fatoração e simplificação, para assim, chegarmos ao resultado (trabalhamos o global); e

C – Buscamos soluções para o conceito de limite de várias maneiras, mostramos para que serve o limite e, apresentamos quais outras disciplinas o limite é considerado fundamental e aplicável (trabalhamos a complexidade).

4.3.1. Módulo 1: Noção Intuitiva de Limite e seus Cálculos

Iniciemos o conteúdo contextualizando um exemplo, pois segundo Morin (2000), a contextualização é condição essencial da eficácia do funcionamento cognitivo.

Gráfico 1
Apresentação da função f(x) = x²

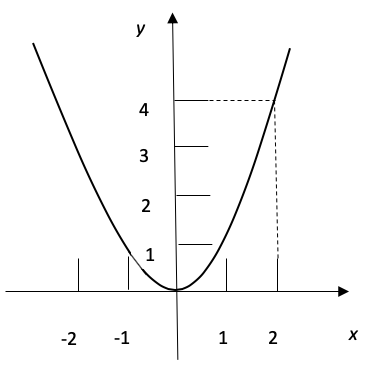
Fonte: Elaborado pelo autor

Figura 2
Calculo de limite por tabelas de aproximação

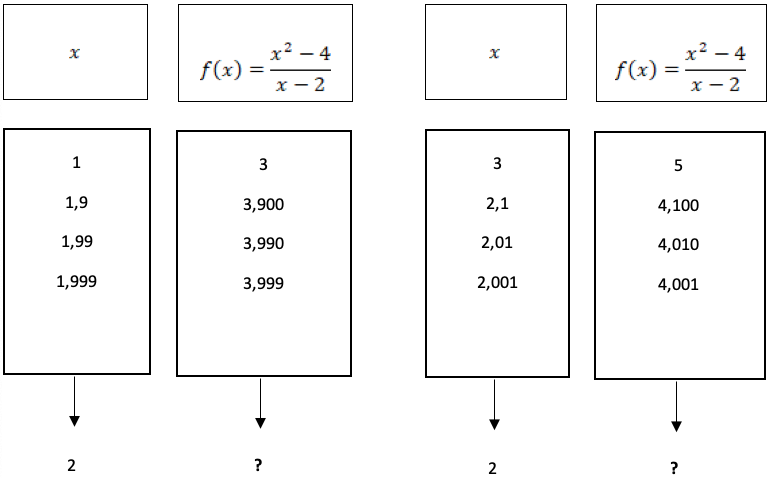
Fonte: Elaborado pelo autor

4.4. Etapa 4: Produção Final

O Produto Final (da sequência didática) é o momento do aluno colocar em prática tudo o que foi trabalhado no módulo. Desta maneira, aconselhamos os alunos a fazerem os exemplos presentes nos livros (citados na referência da Tabela 1), como forma de colocar em prática toda a teoria apresentada.

Ensinar matemática é uma tarefa desafiadora para quem deseja alcançar o objetivo de inserir conhecimentos na formação do aluno, ou seja, é educar; e educar significa ajudar a desenvolver no aluno à curiosidade, a motivação, o gosto por aprender. Diante disso, se faz necessário práticas pedagógicas que tenham significados para os alunos, sendo o professor apenas o mediador da aprendizagem, ou seja, aquele que instiga o desenvolvimento da aprendizagem utilizando-se de estratégias que contribuam para a construção do conhecimento. Tal estratégia, analisada neste artigo, foi estudar limites inspirado na teoria de Morin, seguindo os passos de uma sequência didática. Para tanto, procuramos dar ênfase à etapa “módulo” desta sequência didática.

No módulo, procuramos trabalhar além da teoria matemática de limite, procuramos fazer uma contextualização (contexto) para que o aluno entenda a noção de limite, e a partir disto, tentamos mostrar que para resolver o limite de uma função, existe a necessidade de sabermos o conceito de função, potencialização, produtos notáveis, fatoração e simplificação, ou seja, precisamos saber como calcular as partes para que se  possa chegar ao resultado (o todo). Além disto, trabalhamos outras maneiras de se calcular limite e finalizamos explicando para os alunos o que realmente é o limite e para que serve o limite, tecendo toda a ideia do conteúdo trabalhado (complexidade).

Finalizando nossa conclusão, salientamos a importância da teoria de Morin (2000) neste trabalho, o qual serviu de guia na elaboração do conteúdo de limite, durante toda a sequência didática apresentada, cujo propósito é despertar e facilitar a aprendizagem matemática no aluno.

CURY, H. N. (2006). Análise de erros em disciplinas matemáticas de cursos superiores. Anais do SIPEM. III Seminário Internacional de Pesquisa em Educação Matemática, Águas de Lindóia: SBEM.

DOLZ J.; NOVERRAZ, M.; SCHNEUWLY, B. (2004). Sequências didáticas oral e escrita: apresentação de um procedimento. In: Gêneros orais e escritos na escola. Trad. e (Org.). de Roxane Rojo e Glaís Sales Cordeiro. Campinas-SP: Mercado de Letras, p. 95-128.

FERREIRA, D. H. L.; BRUMATTI, R. N. M. (2009). Um olhar voltado para alunos com dificuldades em Matemática num curso de Engenharia Elétrica. Anais do VI Congresso Iberoamericano de Educación Matemática. Puerto Montt, Chile, p. 949-955.

LIVRONAUTAS. (2018). Biografia de Edgar Morin. Recuperado em 12 de dezembro de 2018 em http://www.livronautas.com.br/ver-autor/365/edgar-morin.

MORIN, E. (2000). Os sete saberes necessários à educação do futuro. Tradução de Catarina Eleonora F. da Silva e Jeanne Sawaya: revisão técnica de Edgard de Assis Carvalho. 2 ed. São Paulo: Cortez. Brasília, DF: UNESCO.

MORIN, E. (2011). Biografia - Edgar Morin. Recuperado em 12 de dezembro de 2018 em http://www.sme.pmmc.com.br/site2011/index.php?option=com_content&view=article&id=519:biografia-edgar-morin&catid=981&Itemid=123.

PERETTI, L.; COSTA, G. M. T. (2013). Sequência didática na matemática. Instituto de Desenvolvimento Educacional do Alto Uruguai (IDEAU). Revista de Educação do IDEAU, v. 08, n. 17.

SILVA, J. I. G.; FERREIRA, D. H. L. (2009). O uso de tecnologias na disciplina de cálculo diferencial e integral I. Anais do XIV Encontro de Iniciação Científica da PUC-Campinas. 29 e 30 de setembro de 2009.

PASCAL, Pensées. Texto estabelecido por Leon Brunschwicg. Ed. Garneir-Flammarion, Paris, 1976.

1. Doutorando do Programa de Pós-Graduação em Ensino de Ciência e Tecnologia – PPGECT – UTFPR, Ponta Grossa – PR. Email: renatohallal@utfpr.edu.br

2. Doutora, Docente do Programa de Pós-Graduação em Ensino de Ciência e Tecnologia – PPGECT – UTFPR, Ponta Grossa – PR

3. Doutor, Docente do Departamento de Matemática – DAMAT – UTFPR, Ponta Grossa – PR

4. Especialista em Tecnologia Java. Técnico Administrativo – UFFS, Realeza – PR