

 Vol. 41 (Nº 02) Año 2020. Pág. 18
Vol. 41 (Nº 02) Año 2020. Pág. 18
PIZARRO-RENDIC, Luis 1; ARAVENA, María 2; RODRÍGUEZ, Marcelo 3 y DÍAZ-LEVICOY, Danilo 4
Recibido: 27/09/2019 • Aprobado: 11/01/2020 • Publicado 31/01/2020
RESUMEN: El propósito del trabajo es evaluar el impacto de una intervención de aula para el aprendizaje de la función racional, bajo la óptica de la visualización, con el apoyo del software educativo Grape. La intervención constó de cuatro sesiones de trabajo, más la aplicación de un pre y un post-test. Los resultados permiten observar una mejora en la comprensión del objeto matemático en estudio, por parte de los estudiantes, luego de finalizar la instrucción. |
ABSTRACT: The purpose of the work is to evaluate the impact of the classroom intervention for learning the rational function, under the optics of visualization with the support of educational software Grape, the intervention consisted of four work sessions, plus the application of the pre and post-test. The results allow to observe that after the intervention the understanding of the object was improved mathematician in study, by the students, after completing the instruction. |
Un tema importante dentro del estudio de la matemática es el de la función (Boyer 1996; De Guzmán, 1974; Zuñiga, 2009); especialmente en las carreras de ingeniería, porque es una herramienta importante para la resolución de problemas que se modelan por medio de este objeto matemático. Por esto, se hace necesario que los estudiantes adquieran habilidades para transitar por las diferentes formas de representar una función (lenguaje numérico, algebraico o gráfico).
La enseñanza de la función bajo un solo enfoque y una visión estática, limitan su aprendizaje, la que debe ser estudiado de una perspectiva variacional, porque al dar una excesiva importancia a cuestiones algorítmicas se pierde la perspectiva de lo conceptual y de las aplicaciones en otras ramas diferentes a la matemática (García, 1997).
En el estudio de la función, en forma variacional, entra en juego la visualización matemática, promoviendo una interacción entre representaciones para la mejor comprensión de los objetos matemáticos involucrados (Hitt, 1998).
Por otro lado, las nuevas tecnologías han impactado en los procesos de enseñanza y aprendizaje de los estudiantes de diferentes niveles educacionales (e.g., Aguilar, 2012; Díaz-Levicoy, 2013; Hernández, 2017), proporcionando nuevos espacios y herramientas. Del mismo modo como los programas computacionales constituyen un importante recurso de apoyo para la enseñanza de la matemática en general y de las funciones en particular, en un ambiente dinámico.
De acuerdo con lo anterior, se diseña e implementa una propuesta de enseñanza de la función racional apoyado por el software matemático Grapes en un curso de cálculo para la carrera de ingeniería de la Universidad Autónoma de Chile sede Talca; para abordar el siguiente objetivo: analizar los procesos de visualización en el aprendizaje de la función racional en estudiantes de primer año de ingeniería antes y después del uso del software educativo Grapes.
Este trabajo se ha estructurado en los siguientes apartados: en la Sección 2 se describen los elementos teóricos, en la Sección 3 los antecedentes, en la Sección 4 se muestras los elementos metodológicos, en la Sección 5 se detallan los resultados principales, y en la Sección 6 se proporcionan las conclusiones del estudio.
En este trabajo utilizamos la teoría de las representaciones de Duval (2004). Este autor señala que las representaciones semióticas utilizadas, normalmente en matemática, no se generan de manera aislada, sino que pertenecen a sistemas de representación que tienen su propia estructura interna, sus propias limitaciones de funcionamiento y de significado, que pueden ser caracterizadas en función de las actividades cognitivas que realice el estudiante.
Según Duval (1994) una representación corresponde a la escritura, notación o símbolo que presenta un objetivo matemático (número, función, figuras, segmento, punto, etc.) enfatizando en que no se debe confundir estos con su representación, que es un punto clave para la compresión de la matemática. Este autor, describe dos tipos de representaciones, las mentales y las semióticas. Las mentales abarcan las imágenes y concepciones que tiene un individuo sobre un determinado objeto matemático. Las semióticas están formadas por signos de un mismo sistema de representación, limitando, de cierta manera, su significado.
Las representaciones mentales y semióticas permiten entender el proceso de comprensión de un concepto u objeto matemático (Duval, 1993). Las representaciones semióticas juegan un papel importante, ya que los objetos matemáticos no son asequibles directamente, sino que se trabajan por medio de signos, dibujos, generando imágenes mentales, que para Vinner y Dreyfus (1989) corresponde al conjunto de todas las estructuras cognitivas que están asociadas con el concepto dado, lo que incluye figuras mentales, propiedades asociadas y procesos.
De este modo, Duval afirma que las representaciones no solamente son necesarias para fines de comunicación, sino que son igualmente esenciales para la actividad cognitiva del pensamiento.
Para conseguir la formación de una representación identificable, se deben considerar dos aspectos, selección de la representación para trabajarla y su uso, de acuerdo con las reglas de formación, las que se detallan a continuación:
La conversión de una representación. Se refiere a la transformación de una representación de un registro a otro, es decir, es una transformación externa al registro de partida. Por ejemplo, la expresión algebraica de una función puede ser representada por una parábola en los ejes coordenados o en un conjunto de datos organizados en un registro tabular. En estas representaciones no se abandona el concepto de función, solo cambio su registro.
El tratamiento de una Representación. Se refiere a una transformación de una representación que se realiza dentro del mismo registro donde ha sido formada, es decir, es una transformación interna (Duval, 1999). Por ejemplo, el cuadrado de binomio se puede ver como un producto de binomios, o como un polinomio al aplicar la ley distributiva de los números reales.
La visualización es un campo de investigación de creciente importancia en Didáctica de la Matemática. Sin embargo, el estudio de su naturaleza y relación con otras formas de registro sigue siendo tema de interés. Por otro lado, las gráficas han ocupado un lugar importante en el campo de la investigación matemática (Zimmerman y Cunningham, 1991), ya que muchos de sus procesos incluyen su construcción y/o interpretación. La construcción se refiere a la elaboración de una gráfica a partir de una representación algebraica o de datos de una tabla. La interpretación se refiere a la capacidad para leer y dar sentido a una gráfica (Leinhardt, Zaslavsky y Stein, 1990). La interpretación de gráficas requiere de procesos agudos de visualización, aunque muchos estudiantes se limitan al trabajo algorítmico (Eisemberg y Dreyfus, 1991).
Para muchos investigadores, la visualización es de gran importancia en el estudio de las funciones, ya que, en la observación instantánea de la gráfica de una función, por más compleja que esta sea, se moviliza en el estudiante, una variedad de preguntas vinculadas a los cambios de registros de representaciones semióticas, y que De la Rosa (2003) señala como uno de los obstáculos epistemológicos más relevantes en la aprehensión del concepto de función. Como se sabe, las ideas, conceptos y métodos de la matemática presentan una gran riqueza de contenidos visuales, representables intuitivamente, cuya utilización resulta muy provechosa para la resolución de problemas (Guzmán, 1996).
En matemática se utilizan diferentes representaciones que requieren de la visualización, por ejemplo, en el análisis de las funciones es usual manejar representaciones para describir propiedades como la paridad, la periodicidad y la traslación de funciones. Es importante entender cómo los alumnos perciben las funciones reales, es decir, qué códigos usan para descifrar y procesar información visual. De allí la importancia de explorar las habilidades visuales que se necesitan para aprender el concepto de función. Por eso es importante estudiar las funciones reales en ambientes computacionales (Cordero, Muñoz, Ruiz y Suárez, 2000).
La visualización en matemática no es lo mismo que psicología, el uso que se hará aquí de este término difiere del que se hace en el lenguaje cotidiano, donde se relaciona más con la formación de imágenes que con la construcción, ya sean éstos realizados con lápiz y papel o con la ayuda de un software educativo asociados a un concepto o problema matemático que permitan su comprensión o resolución de un problema (Cantoral y Montiel, 2001).
En Didáctica de la Matemática, son diversos los autores que han tratado de definir el concepto de visualización (e.g., Arcavi, 2003; Cantoral, Farfán, Cordero, Alanís, Rodríguez. Garza, 2000; Duval, 1999; Gutiérrez, 1996; Hitt, 1995; Zimmermann y Cunningham, 1991). Entre los elementos comunes de estas definiciones se encuentra el proceso de formar imágenes mentales para representar, comunicar, documentar y transformar sobre el papel o con herramientas tecnológicas una idea matemática. Además, Duval (1999) menciona que la visualización se refiere a la capacidad de reconocer las unidades significativas de los registros para pasar de una representación a otra en forma bidireccional: por lo tanto, es necesario desarrollar las tres capacidades relacionadas con la semiósis: formación, tratamiento y conversión.
La captación visual es uno de los caminos para acercarnos a los objetos. Pero este acercamiento no implica que se realicen operaciones con los objetos y que haya discriminación en sus propiedades. La captación visual, en algunas ocasiones, puede perturbar la aprehensión del objeto. En muchas ocasiones esto tiene que ver con los tipos de imágenes que se establezcan en los individuos. Cuando se trata de hacer traslaciones del mundo físico a uno gráfico o algebraico algunas veces surgen dificultades. Ciertos elementos figurales provocan que el estudiante se dirija a respuestas erróneas. En una investigación que realizó Hitt (1995) observó que, en las respuestas de los profesores, la forma de la figura del recipiente les inducía hacia cierta gráfica sin realizar un análisis sobre las variables en juego lo que él consideró un obstáculo que impide la captura de la situación o el objeto.
La educación en los últimos años, en el contexto de la Sociedad de la Información y del Conocimiento, se ha visto fuertemente influenciada por la incorporación de las tecnologías que se han presentado como un recurso para mejorar y renovar los procesos educativos (Brunner, 2003).
Las Tecnologías de la Información y la Comunicación (TIC) evolucionan asombrosamente día a día, debido a su característica principal de interconexión a través de la Red, lo que ha generado un gran impacto en la organización de la instrucción (Cabero-Almenara, 2010; Gargallo, 2018; Marquès, 2000, 2013; Morales, Trujillo y Raso, 2015). Integrar las TIC a la educación, permite contribuir a la alfabetización computacional del estudiante, mejorar la productividad, aprovechar sus ventajas al innovar en la práctica pedagógica y reducir el fracaso escolar (Marqués, 2000).
Existen varias razones que fundamentan y promueven la integración de las TIC en el marco educativo, su uso permite modificar el modelo de enseñanza, es decir, los alumnos son los protagonistas de la actividad de aprendizaje, estimulando el desarrollo de un aprendizaje autónomo (Araujo, Bonilla y Cifuentes, 2016; Martínez-Fernández y Rabanaque, 2008). Otra razón que es necesaria para satisfacer las exigencias que emanan de una nueva sociedad de la información y comunicación, es la alfabetización digital que consiste en que los alumnos deben adquirir las competencias básicas en el uso de las TIC, que a su vez pueden mejorar la productividad, al procesar y difundir información, otro motivo para considerar las TIC es la innovación pedagógica al aprovechar la gama de posibilidades didácticas que estas herramientas tecnológicas ofrecen para lograr una educación más eficaz e inclusiva (Marqués, 2000)
La integración de las TIC, con orientaciones pedagógicas conlleva a crear nuevos escenarios en los cuales, se activa el aprendizaje constructivo (Martínez-Fernández y Rabanaque, 2008;
Sánchez, Salinas, Purcell y Pérez, 2008), en el cual los alumnos como docentes modifican sus roles, es decir, los estudiantes pasan de ser pasivos a activos y los docentes se convierten en mediadores u orientadores del proceso educativo. Una buena práctica pedagógica con uso de TIC, puede producir, nuevas estrategias para la construcción de conocimientos en los procesos educativos en el aula (Cabero-Almenara, 2010).
Kulik (2003) destaca que los estudios de evaluación sugieren que las TIC están volviéndose cada vez más eficaces para apoyar la enseñanza en niveles básicos y secundarios, lo que no resulta sorprendente al ver que los computadores han mejorado dramáticamente durante las tres últimas décadas: son más rápidos, más amistosos, más gráficos y fonéticos que los modelos de antes.
El software educativo Grapes, es un programa gráfico desarrollado en CRICED (Centro de Investigación en Cooperación Internacional para el desarrollo Educativo de la Universidad de Tsukuba, Japón). Grapes es un editor gráfico, interactivo, que puede ser usado como una ayuda para dibujar curvas matemáticas, al mismo tiempo que ha sido diseñado para ser extremadamente simple en su uso. La disponibilidad de este programa permite analizar las funciones desde sus respectivas gráficas.
En Didáctica de la Matemática, uno de los contenidos que ha centrado el interés de diversos investigadores es el de función (e.g., Zuñiga, 2009). Así lo demuestran los estudios realizados en diferentes niveles de formación, como Educación Secundaria (e.g., Deulofeu, 2001), formación de profesores (Parra-Urrea y Pino-Fan, 2017) o estudiantes de ingeniería (Zuñiga, 2007).
De esta manera, por ejemplo, encontramos el estudio de Duval (1992), donde abordó la representación gráfica y algebraica de la ecuación de la recta, evidenciando la dificultad que presenta el traspaso entre estas representaciones. Más tarde, Guzmán (1998) analizó las respuestas a un cuestionario de estudiantes de primer año de ingeniería, observando que estos trabajan en un solo registro, el algebraico, y con esto una clara manifestación de falta de articulación entre las representaciones de una función.
Por otra parte, Hitt (1994) plantea que la aprehensión del concepto de función es un proceso complejo y que se ve dificultado por tres tipos de obstáculos, de corte epistemológico, didáctico y la concepción que los profesores de matemática trasmiten a sus estudiantes. Señala, además, que a través de las funciones podemos modelar fenómenos de la vida real (Hitt, 2009).
Respecto de la matemática escolar, el concepto de función es uno de los más difíciles de enseñar, debido a la multitud de objetos matemáticos que lleva asociados (e.g., Carlson, 1998, 2002; Selden, Selden, Hauk y Mason, 2000; Zandieh, 2000), entre ellos: pendiente, tangente, variación, velocidad, límite y derivada. Entender la idea de función implica, asociar estos y otros elementos (Abrate, Pochulu y Vargas, 2006).
En cuanto al tema de visualización, nos encontramos con la tesis de Ramírez (2012), donde se expone la definición y elementos de visualización en base a las investigaciones basado en trabajos anteriores (e.g., De Guzmán, 1996; Gutiérrez, 2006). Asimismo, en el año 2012 investigación realizada por Gatica (2012) quien indica la importancia de la visualización en el aprendizaje de conceptos matemáticos.
Autores como Cantoral y Montiel (2001) definen visualización, y citan a Presmeg (1986) quien realiza una clasificación de las imágenes mentales. Además, nos encontramos con el trabajo de Gutierrez y Parada (2007), quienes recopilan las visiones de Duval (1992, 1999, 2004), Hiebert y Carpenter (1992), Hitt (1996), Peralta (2002) y Romero (2000) quienes aportan para entender la teoría de visualización y representaciones de una función.
Nos encontramos que todas estas investigaciones son de corte internacional, con respecto a nivel nacional no se encuentra bibliografía referente a visualización de funciones. Sin embargo, existen estudios referentes a modelización matemática, en los que se encuentran las investigaciones de Aravena y cols. (Aravena, 2011; Aravena y Caamaño, 2007; Aravena, Caamaño y Giménez, 2008), quienes presentan el proceso de modelación y sus respectivas etapas, además de los criterios para evaluar este proceso en los estudiantes.
El estudio es de un tipo cuasi experimental y con un diseño longitudinal (Hernández, Fernández y Baptista, 2014), considerando la implementación de una intervención de aula y la aplicación de un pre y post-test, previa validación de expertos (3).
La muestra estuvo formada por 30 estudiantes (13 mujeres y 17 hombres), con edades entre 19 y 22 años, y pertenecen a uno de los dos grupos de primer año de la carrera de Ingeniería de la Universidad Autónoma de Chile (Talca).
Mediante una prueba escrita se buscó recoger información sobre el conocimiento de los estudiantes de primer año de ingeniería, antes y después de la intervención de aula. Las respuestas otorgadas a cada una de las preguntas, permite determinar el factor de logro que alcanzan los participantes en cada una de ellas.
Este instrumento constó de 50 puntos, distribuidos en 5 preguntas (Tabla 1) con 10 puntos en cada respuesta correcta. La tabulación se realizó a partir de la cuantificación de los puntos obtenidos al desarrollar cada pregunta.
Tabla 1
Descripción de los instrumentos
Pregunta |
Objetivo |
1 |
Identificar y graficar a través de dos funciones afín, f y g. Encontrar la gráfica de f/g. |
2 |
Reconocer y determinar en una función racional, las características de ella. |
3 |
Identificar en una expresión gráfica de una función racional sus respectivas características. |
4 |
Reconocer en una tabla de valores, las características de una función que se ajuste a los datos de la tabla. |
5 |
Analizar y resolver problemas reales en los que se requiera de la aplicación del concepto de función racional. |
La intervención de aula se desarrolló en el curso de introducción al cálculo (precálculo), mediante la aplicación de actividades de laboratorio individual o grupal con el objetivo de introducir a los estudiantes a la visualización matemática, en el contenido de funciones, a través del software educativo Grapes, recurso educativo que complementa la acción del profesor. Con el uso de este software, se persigue incentivar el autoaprendizaje y la cooperación a través de la búsqueda, el desarrollo y la transferencia a problemas que constituyen aplicaciones concretas al tema de funciones.
Las actividades de aprendizaje, para trabajar las funciones, sus representaciones gráficas y problemas asociados a la función racional, se desarrollaron en un laboratorio computacional con 45 equipos y una pizarra interactiva donde podrían interactuar con el software Grapes y las representaciones involucradas.
Para trabajar con el concepto de función, durante la intervención de aula, se plantearon actividades como las mostradas en la Figura 1. En ella, se aborda la idea de que una función es aquella en que cada elemento del eje de las abscisas (dominio) tiene una única imagen en el eje de las ordenadas (recorrido).
Figura 1
Reconocer una función
con su dominio y recorrido
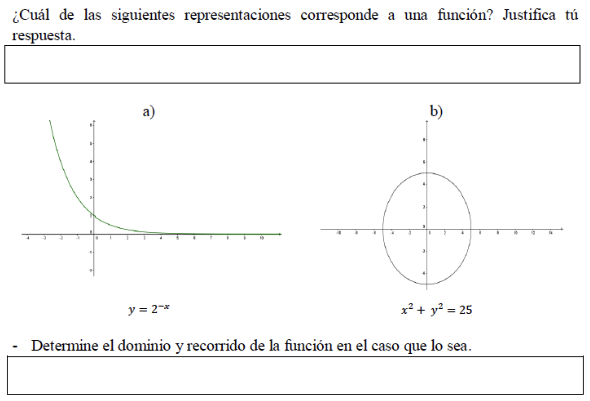
Otro tipo de actividad que desarrollaron los estudiantes es la mostrada en la Figura 2. En ella, debieron evaluar los valores indicados en la primera fila de tabla en las funciones de la primera columna (f(x) y g(x)). Posteriormente, debieron graficar los pares ordenados encontrados y, de acuerdo con lo observado, mencionar las diferencias entre ambas gráficas.
Figura 2
Construcción de
la función racional
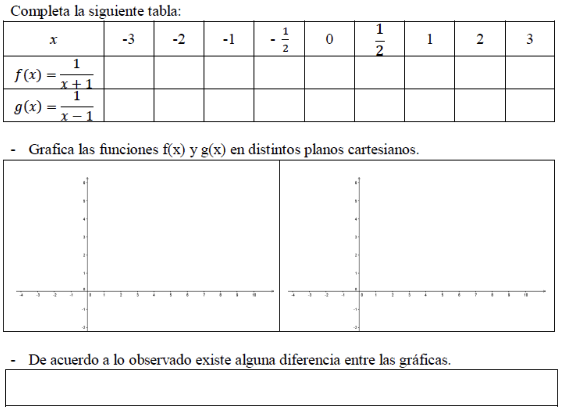
También, se plantean actividades para trabajar con el software educativo Grapes, como la mostrada en la Figura 3. En ella, se entrega un listado de funciones racionales, para ser ingresadas al software y obtener las respectivas gráficas. Y, en este caso, apreciar las diferentes formas gráficas que puede tomar una función de esta naturaleza.
Figura 3
Gráficas de función racional para
trabajar con apoyo de Grapes

En la Tabla 2 se realiza un análisis exploratorio de las habilidades en el pre-test, donde la de modelar es la que obtiene un mayor porcentaje de logro (25%), con un valor mínimo de 0% y un máximo de 60%, le sigue la habilidad de argumentar y comunicar (17,3%), donde el máximo porcentaje de logro es de 40%. Por otro lado, las habilidades de resolver problemas y representar son las menos logradas, con un porcentaje medio de logro de 8,3%.
Tabla 2
Análisis exploratorio de las habilidades
matemáticas del pre-test
Habilidad |
N |
Mínimo |
Máximo |
Media |
Desv. Est. |
Modelar |
30 |
0 |
60 |
25 |
15,702 |
Argumentar y comunicar |
30 |
0 |
40 |
17,3 |
12,015 |
Resolver problemas |
30 |
0 |
40 |
8,3 |
9,855 |
Representar |
30 |
0 |
40 |
8,3 |
11,769 |
En la Tabla 3 se muestran los resultados del post-test respecto al logro de las habilidades. En ella observamos que las habilidades más logradas son las de modelar (95,3%) y de argumentar y comunicar (89,7%); manteniendo la tendencia del pre-test. Las habilidades de representar y resolver problemas son las menos logradas, con un porcentaje medio de éxito de 65,7% y 54,8%, respectivamente. Estas últimas cambian de orden con respecto al pre-test, es decir, la habilidad que presenta mayor dificultad es la de resolver problemas y no la de representar. Además, vemos que la habilidad de resolver problema es la única que no presenta, al menos un estudiante, con todas respuestas correctas.
Tabla 3
Análisis exploratorio de las habilidades
matemáticas del post-test
Habilidad |
N |
Mínimo |
Máximo |
Media |
Desv. Est. |
Modelar |
30 |
40 |
100 |
95,3 |
13,322 |
Argumentar y comunicar |
30 |
60 |
100 |
89,7 |
16,709 |
Representar |
30 |
20 |
100 |
65,7 |
28,730 |
Resolver problemas |
30 |
20 |
90 |
54,8 |
18,914 |
En la Figura 4 se muestra el porcentaje de logro de la habilidad matemática del pre-test y post-test de los estudiantes que participaron en la intervención de aula. En el lado izquierdo se representan el porcentaje de logro del pre-test y en el derecho el porcentaje de logro del post-test, y donde la magnitud de la línea nos dice el cambio porcentual de cada estudiante. Se observa que los estudiantes 6 y 25 obtuvieron el menor de los cambios en su puntuación. Por el contrario, los estudiantes 16 y 27 son los que presentan mayor variación porcentual en el pre-test y post-test.
Figura 4
Logro de cada estudiante
en pre-test y post-test
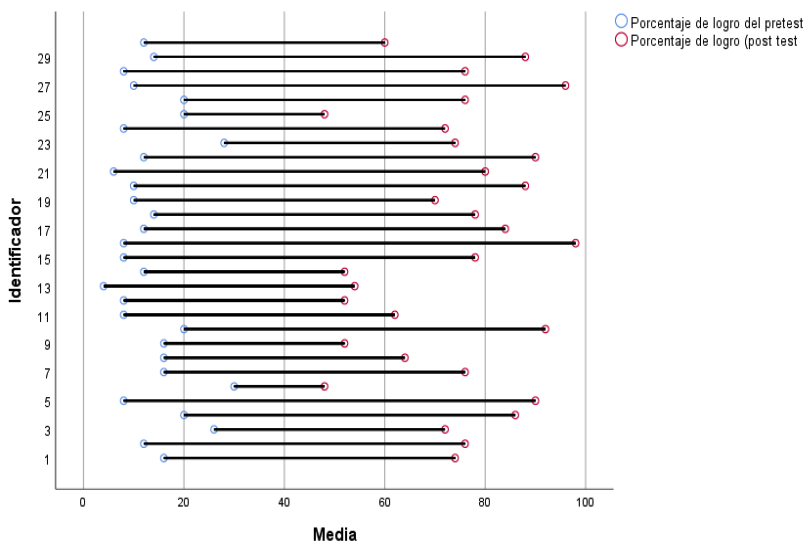
Para un nivel de significancia del 5% existe suficiente evidencia muestral para afirmar que le porcentaje de logro en la habilidad matemática para el post-test es superior al porcentaje de logro obtenido en el pre-test (t=-19,142; valor-p<0,001). Lo que indica que existen cambios altamente significativos de los porcentajes de logro de los estudiantes en el pre-test y post-test, atribuible a la intervención de aula.
Dada las dificultades que presenta el aprendizaje del concepto de función para los estudiantes de diferentes niveles de enseñanza (e.g., Prada-Núñez, Hernández-Suarez y Jaimes-Contreras, 2017), así como su utilidad en diferentes disciplinas, es que nos planteamos la idea de realizar una intervención de aula para trabajar el concepto de función racional y su visualización en estudiantes de ingeniería, con apoyo de un software educativo de acceso libre (Grapes).
En esta intervención, reforzamos el concepto de función desde los puntos de vista verbal y gráfico, para luego trabajar la función racional desde sus diferentes representaciones (tabular, gráfico y verbal), con apoyo del software Grapes.
La intervención pedagógica constó de cuatro sesiones de aprendizaje, mediadas por el software Grapes, permitiendo una mejora en la visualización de la función racional, así como trabajar distintas formas gráficas de esta, donde el numerador y denominador pueden ser polinomios hasta de grado dos.
Con lo anterior se concluye que el uso del software educativo ayudó a la mejorar la comprensión de la función racional, porque los estudiantes pudieron visualizar cómo se comporta la gráfica de la mencionada función y establecen ciertas regularidades, ya que les permitió ensayar y experimentar, utilizaron diferentes estrategias, tales como comparar, modelar, ensayo y error, fomentando el pensamiento reflexivo, crítico y creativo.
Respecto de las habilidades matemáticas, descritas en las directrices curriculares de Enseñanza Media y los planes de estudio de los futuros ingenieros participantes en esta investigación, vemos un avance significativo en los porcentajes de logro, por ejemplo, la habilidad de modelar transitó de un 25% a un 95,3%, siendo también la mejor lograda en el pre-test y post-test. La habilidad de resolver problemas es la que obtiene los porcentajes de logro más bajos, distanciándose de representar en el post-test. Dificultad reconocida por la comunidad científica (e.g., Díaz y Poblete, 2009).
Dado que estos resultados son positivos, se pretende profundizar en aspectos de la visualización, como por ejemplo trabajar el paso de la gráfica de una función a su expresión algebraica, potenciándola como una herramienta didáctica que facilite la aproximación a los objetos matemáticos.
Abrate, R., Pochulu, M. y Vargas, J. (2006). Errores y dificultades en Matemática: análisis de causas y sugerencias de trabajo. Buenos Aires: Universidad Nacional de Villa María.
Aguilar, M. (2012). Aprendizaje y Tecnologías de Información y Comunicación: Hacia nuevos escenarios educativos. Revista Latinoamericana de Ciencias Sociales, Niñez y Juventud, 10(2), 801-811.
Aravena, M. (2011). Una propuesta de intervención en prácticas tempranas. Modelización de situaciones. En R. Borba, C. Monteiro y A. Ruiz (Eds.), Anais da XIII Conferência Interamericana de Educação Matemática (pp. 1-12). Recife: Universidad Federal de Pernambuco.
Aravena, M. y Caamaño, C. (2007). Modelización matemática con estudiantes de secundaria de la comuna de Talca, Chile. Estudios Pedagógicos, 33(2), 7-25.
Aravena, M., Caamaño, C. y Giménez, J. (2008). Modelos matemáticos a través de proyectos. RELIME. Revista Latinoamericana de Investigación en Matemática Educativa, 11(1), 49-92.
Araujo, M., Bonilla, M. E., y Cifuentes, S. (2016). Estrategias lúdicas mediadas por tic para favorecer el aprendizaje autónomo (Trabajo de Especialistas en Pedagogía de la Lúdica). Fundación Universitaria los Libertadores, Colombia.
Arcavi, A. (2003). The role of visual representations in the learning of mathematics. Educational Studies in Mathematics, 52(3), 215-241.
Boyer, C. B. (1996). Historia de la matemática. Madrid: Alianza.
Brunner, J. J. (2003). La educación al encuentro de las nuevas tecnologías. En J. J. Brunner y
J. C. Tedesco (Eds.), Las nuevas tecnologías y el futuro de la educación (pp. 15-67). Buenos Aires: IIPE-UNESCO.
Cabero-Almenara, J. (2010). Los retos de la integración de las TICs en los procesos educativos. Límites y posibilidades. Perspectiva Educacional, 49(1), 32-61.
Cantoral, R. Farfán, R., Cordero, F. Alanís, J. A. Rodríguez, R. A. y Garza, A. (2000). Desarrollo del pensamiento matemático. México: Trillas.
Cantoral, R. y Montiel, G. (2001). Funciones: visualización y pensamiento matemático. México: Prentice Hall & Pearson Edución.
Carlson M. (1998). A Cross-Sectional Investigation of the Development of the Function Concept. Research in Collegiate Mathematics Education, 7, 114-162.
Carlson, M. P. (2002). Physical enactment: a powerful representational tool for understanding the nature of covarying relationships?. En F. Hitt (Ed.), Representations and mathematics visualization (pp. 63-77). México: Cinvestav-IPN.
Cordero. F., Muñoz. G., Ruiz. B. y Suárez, L. (2000). Diseño de situaciones del cálculo. El comportamiento tendencial de las funciones: la linealidad del polinomio. En R. Cantoral, R. Farfán, F. Cordero, J. A. Alanís, R. A. Rodríguez y A. Garza (Eds.), Desarrollo del pensamiento matemático (pp. 62-80). México: Trillas.
De Guzmán, M. (1974). Matemáticas en un mundo moderno. Madrid: Bluna.
De la Rosa, A. (2003). Errores e inconsistencias en la enseñanza del concepto de función en el docente: el grado de visualización. Memorias XIII Semana Regional de Investigación y Docencia en Matemáticas (pp. 121-133). Hermosillo: Universidad de Sonora.
Deulofeu, J. (2001). Las funciones en la educación secundaria: ¿para qué?, ¿cómo? aportaciones de la investigación. Actas X Jornadas para la Enseñanza y el Aprendizaje de las Matemáticas (pp. 367-377). Zaragoza: Federación Española de Sociedades de Profesores de Matemáticas.
Díaz, V. y Poblete, A. (2009). Perfeccionamiento en matemáticas basado en competencias para docentes de escuelas básicas municipalizadas de la región de Los Lagos y de Los Ríos. Estudios Pedagógicos, 35(2), 13-34.
Díaz-Levicoy, D. (2013). TIC en Educación Superior: ventajas y desventajas. Educación y Tecnología, 4, 44-50.
Duval, R. (1993). Semiosis y noesis. En E. Sánchez y G. Zubieta (Eds.), Lecturas en didáctica de la matemática: Escuela Francesa (pp. 118-144). México: Sección de Matemática Educativa del CINVESTAV-IPN.
Duval, R. (1994). Les différents fonctionnements d’une figure dans une démarche géométrique. Repères Irem, 17, 121-138.
Duval, R. (1995). Sémiosis et pensée humaine: registres sémiotiques et apprentissages intellectuels. Berne: Peter Lang.
Duval, R. (1998). Registros de representación semiótica y funcionamiento cognitivo del pensamiento. En F. Hitt (Ed.), Investigaciones en Matemática Educativa (Vol. 2, pp. 173-201). México: Grupo Editorial Iberoamérica.
Duval, R. (1999). Representation, vision and visualization: cognitive functions in mathematical thinking. Basic issues for learning. En F. Hitt y M. Santos (Eds.), Proceedings of the 21st North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 2-26). Cuernavaca: The International Group for the Psychology of Mathematics Education.
Duval, R. (2004). Semiosis y pensamiento humano: registros semióticos y aprendizajes intelectuales. Cali: Universidad del Valle.
Duval, R. (1992). Gráficas y Ecuaciones: la articulación de dos registros. En E. SÁnchez (Ed.), Antología en Educación Matemática (pp. 125-139). México: Sección de Matemáticas Educativa del CINVESTAV-IPN.
Eisenberg, T. y Dreyfus, T. (1991). On the reluctance to visualize in mathematics. En W. Zimmermann y S. Cunningham (Eds.), Visualization in teaching and learning mathematics (pp. 25-37). Washington, DC: Mathematical Association of America.
García, M. M. (1997). Conocimiento profesional del profesor de matemáticas. El concepto de función como objeto de enseñanza-aprendizaje. Sevilla: Universidad de Sevilla
Gatica, S. N. y Ares, O. E. (2012). La importancia de la visualización en el aprendizaje de conceptos matemáticos. EDMETIC, 1(2), 88-107.
Gutiérrez, A. (1996). Visualization in 3-Dimensional Geometry: In Search of a Framework. En L. Puig y A. Gutierrez (Eds.), Proceedings of the 20th International Conference for the Psychology of Mathematics Education (pp. 3-19). Valencia: Universidad de Valencia.
Guzmán, I. (1998). Registros de Representación, el aprendizaje de nociones relativas a funciones: voces de estudiantes. RELIME. Revista Latinoamericana de Investigación en Matemática Educativa, 1(1), 5-21.
De Guzmán, M. (1996). Sobre el papel del matemático en la educación matemática. En C. Alsina, J. M. Alvarez, M. Niss, A. Perez, L. Rico y A. Sfard (Eds.), Proceedings of the 8th International Congress on Mathematical Education (pp. 47-63). Sevilla: Sociedad Andaluza de Educación Matemática Thales.
Gargallo, A. F. (2018). La integración de las TIC en los procesos educativos y organizativos. Educar em Revista, 34(69), 325-339.
Hernandez, R. M. (2017). Impacto de las TIC en la educación: retos y perspectivas. Propósitos y Representaciones, 5(1), 325 – 347
Hernández, R., Fernández, C. y Baptista, P. (2014). Metodología de la investigación. México: McGrall Hill.
Hiebert, J. y Carpenter, T. (1992). Learning and teaching with understanding. En D. Grouws (Ed.), Handbook of Research on Mathematics Teaching and Learning (pp. 65-97). New York. NY: Macmillan Publishing Company.
Hitt, F. (1994). Teachers' difficulties with the construction of continuous and discontinuous functions. Focus on Learning Problems in Mathematics, 16(4), 10-20.
Hitt F. (1995). Intuición primera versus pensamiento analítico: dificultades en el paso de una representación gráfica a un contexto Real. Educación Matemática, 7(1), 63-75.
Hitt F. (1996). Sistemas semióticos de representación del concepto de función y su relación con problemas epistemológicos y didácticos. En F. Hitt (Ed.), Investigaciones en Educación Matemática (Vol. 1, pp. 245-264). México: Grupo Editorial Iberoamérica.
Hitt, F. y Cortés, J. C. (2009). Planificación de actividades en un curso sobre la adquisición de competencias en la modelización matemática y uso de calculadora con posibilidades gráficas. Revista Digital Matemática, Educación e Internet, 10(1), 1-30.
Kulik, J. A. (2003). Effects of using instructional technology in elementary and secondary schools: What controlled evaluation studies say. Arlington, VA: SRI International.
Leinhardt, G., Zaslavsky, O. y Stein, M. K. (1990). Functions, graphs, and graphing: tasks, learning, and teaching. Review of Educational Research, 60(1), 1-64.
Marqués, P. (2000). Impacto de las TIC en educación: funciones y limitaciones. Barcelona: Universidad de Barcelona.
Marquès, P. (2013). Impacto de las TIC en la educación: Funciones y limitaciones. 3 c TIC: Cuadernos de Desarrollo Aplicados a las TIC, 2(1), 1-15.
Martínez-Fernández, J. R. y Rabanaque, S. (2008). Autorregulación y trabajo autónomo del estudiante en una actividad de aprendizaje basada en las TIC. Anuario de Psicología, 39(3), 311-331.
Morales, M., Trujillo, J. M. y Raso, F. (2015). Percepciones acerca de la integración de las TIC en el proceso de enseñanza-aprendizaje de la universidad. Pixel-Bit. Revista de Medios y Educación, 46, 103-117.
Parra-Urrea, Y. y Pino-Fan, L. (2017). Conocimiento didáctico-matemático de profesores chilenos sobre la noción de función. En FESPM (Ed.), VIII Congreso Iberoamericano de Educación Matemática. Libro de Actas (pp. 466-474). Jaén: FESPM.
Peralta, J. (2002). Dificultades para articular los registros gráfico, algebraico y tabular: el caso de la función lineal. Memorias de la XII Semana Regional de Investigación y Docencia en Matemáticas (pp. 166-173). Hermosillo: Universidad de Sonora
Prada-Núñez, R. P., Hernández-Suárez, C. A. y Jaimes-Contreras, L. A. (2017). Representación semiótica de la noción de función: concepciones de los estudiantes que transitan del Colegio a la Universidad. Panorama, 11(20), 34-44.
Presmeg, N. (1986). Visualization and mathematical giftedness. Educational Studies in Mathematics, 17(3), 297-311.
Ramírez, R. (2012). Habilidades de visualización de los alumnos con talento matemático (Tesis doctoral). Universidad de Granada, España.
Romero, I. (2000). Representación y comprensión en pensamiento numérico. En L. C. Contreras, J. Carrillo, N. Climent y M. Sierra (Eds.), Cuarto Simposio de la Sociedad Española de Investigación en Educación Matemática (pp. 35-46). Huelva: Universidad de Huelva.
Sánchez, J., Salinas, A., Purcell, O. y Pérez, L. (2008). Buenas prácticas pedagógicas con integración curricular de TICs al interior del aula. En J. Sánchez (Ed.), Nuevas Ideas en Informática Educativa (Vol. 4, pp. 221-231). Santiago: Universidad de Santiago de Chile.
Selden A., Selden J., Hauk S. y Mason A. (2000). Why can’t calculus students access their knowledge to solve non-routine problems? En E. Dubinsky, A. Schoenfeld y J. Kaput (Eds.), Research in Collegiate Mathematics Education. IV CBMS Issues in Mathematics Education (Vol. 8, pp. 128-153). Providence, RI: American Mathematical Society.
Vinner, S. (1989). The avoidance of visual considerations in calculus students. Focus on Learning Problems in Mathematics, 11(1-2), 149-156.
Vinner, S. y Dreyfus, T. (1989). Image and definitions for the concept of function. Journal for Research in Mathematics Education, 20(4), 356-366.
Zandieh M. (2000). A theoretical framework for analyzing student understanding of the concept of derivative. En E. Dubinsky, A. Schoenfeld y J. Kaput (Eds.), Research in Collegiate Mathematics Education. IV CBMS Issues in Mathematics Education (Vol. 8, pp. 103-127). Providence, RI: American Mathematical Society.
Zimmermann, W. y Cunningham, S. (1991). Visualization in teaching and learning mathematics. Washington, DC: Mathematical Association of America.
Zuñiga, L. (2007). El cálculo en carreras de ingeniería: un estudio cognitivo. Revista Latinoamericana de Investigación en Matemática Educativa, 10(1), 145-175.
Zuñiga, M. (2009). Un estudio acerca de la construcción del concepto de función, visualización. En alumnos de un curso de Cálculo I (Tesis de Máster). Universidad Pedagógica Nacional, Honduras.
1. Magister en Didáctica de la Matemática. Facultad de Arquitectura y Construcción, Universidad Autónoma de Chile. E-mail: lpizarror@uautonoma.cl
2. Doctora en Didáctica de la Matemática. Facultad de Ciencias Básicas, Centro de Investigación en Educación Matemática y Estadística, Universidad Católica del Maule. E-mail: maravenadiaz@gmail.com
3. Doctor en Estadística. Facultad de Ciencias Básicas, Universidad Católica del Maule. E-mail: mrodriguezgallardo@gmail.com
4. Doctor en Ciencias de la Educación. Facultad de Ciencias Básicas, Centro de Investigación en Educación Matemática y Estadística, Universidad Católica del Maule. E-mail: dddiaz01@hotmail.com
[Índice]
revistaespacios.com

Esta obra está bajo una licencia de Creative Commons
Reconocimiento-NoComercial 4.0 Internacional