

 Vol. 41 (Nº 13) Año 2020. Pág. 4
Vol. 41 (Nº 13) Año 2020. Pág. 4
PRIETO-RODRÍGUEZ, Germán A. 1 y CABRERA-MOYA, Diego R. 2
Recibido: 05/12/2019 • Aprobado: 31/03/2020 • Publicado: 16/04/2020
RESUMEN: El presente artículo analiza los resultados de la implementación de una lúdica de aprendizaje en el aula, bautizada por los autores como “Apuntando a la simulación” como una estrategia para enseñar los principios básicos de la Simulación de Montecarlo en una asignatura de la línea de Investigación de Operaciones. Se realizó un estudio de tipo exploratorio cuyo objetivo es determinar la percepción de los estudiantes, utilizando una técnica de muestreo no probabilística o circunstancial, mediante un muestreo por conveniencia con 40 estudiantes de los cursos de Distribución de Recursos e Investigación de Operaciones de la Escuela de Administración de la Universidad de Bogotá Jorge Tadeo Lozano. Los resultados positivos obtenidos al evaluar tanto el nivel de comprensión de las temáticas como el nivel de interés de los estudiantes en las mismas son un argumento favorable para continuar su implementación. |
ABSTRACT: This article analyzes the results of the implementation of a playful learning in the classroom, baptized by the authors as "Pointing to simulation" as a strategy to teach the basic principles of Monte Carlo Simulation in a subject of the Research line of Operations. An exploratory study was conducted whose objective is to determine the students' perception, using a non-probabilistic or circumstantial sampling technique, by means of convenience sampling with 40 students of the Resource Distribution and Operations Research courses of the School of Administration of the University of Bogotá Jorge Tadeo Lozano. The positive results obtained when evaluating both the level of understanding of the topics and the level of interest of the students in them are a favorable argument to continue their implementation. |
El proceso de enseñanza-aprendizaje de asignaturas de corte matemático implican un gran reto docente, pues para algunos estudiantes este tipo de contenidos no solo puede resultar aburrido, sino que también en algunos casos se encuentran grandes prevenciones y resistencia al componente matemático, además de que lo suelen considerar poco útil en la vida práctica. La enseñanza tradicional de estos temas suele quedarse entonces en impartir contenidos que son posteriormente evaluados en exámenes que comprueban si el estudiante aprendió ciertos procedimientos o métodos matemáticos, pero que muchas veces no dejan en el estudiante una verdadera comprensión del concepto, de la lógica y la utilidad que realmente tienen ciertos contenidos matemáticos, pues muchos estudiantes se limitan a memorizar esos procedimientos, repetirlos en un examen y olvidar o desechar los conocimientos adquiridos una vez aprueban la asignatura: “Aprendizaje bulímico”, como lo denomina María Acaso (2009).
En el caso de la línea de Producción o de Investigación de Operaciones de la carrera de Administración de Empresas, hemos encontrado que se convierte en uno de los principales obstáculos de los estudiantes para finalizar su plan curricular, pues varios de ellos tienen esa prevención y rechazo por los temas matemáticos, mientras que en egresados o estudiantes de semestres avanzados se encuentran muy pocas evidencias de que estos contenidos hayan sido interiorizados y puedan resultar útiles en la vida profesional. Surge entonces el reto de cómo enseñar temas matemáticos aplicables a la administración de organizaciones, de tal manera que los conceptos básicos se afirmen en el largo plazo. En el caso de esta investigación, buscamos analizar cómo una lúdica de aprendizaje puede contribuir a hacer el proceso educativo más ameno, interactivo y significativo en el largo plazo, en particular para el proceso de enseñanza aprendizaje del método de simulación denominado Método de Montecarlo. En este capítulo introductorio se presenta entonces una descripción de la temática teórica del método en sí mismo y una revisión de qué son y cuál es la utilidad de las lúdicas de aprendizaje, para posteriormente describir la lúdica y la evaluación de la manera en la que fue aplicada en nuestro público objetivo.
Autores como Bullana y Urquía (2009) ubican los antecedentes de la teoría de la simulación en propuestas tales como la teoría de sistemas y la teoría de los servomecanismos. Estas dos teorías basan su funcionamiento en la recolección continua de los resultados de un proceso y de su relación con las condiciones de entrada que los generaron. De esta forma, las condiciones de salida y su relación con las decisiones que se toman encuentran una relación con los resultados obtenidos. Y son estos resultados obtenidos los que permiten a su vez alimentar nuevamente los sistemas como valores de las variables independientes (fenómenos resultantes) que resultan de la interacción de un cierto número de variables dependientes (fenómenos de origen).
Esta lógica permitió desarrollar la teoría de la simulación, la cual Tumay (1996) definen como aquella que plantea las condiciones necesarias para que un problema de la vida real pueda ser reproducido en un modelo detallado, que a su vez permita determinar la reacción o respuesta del sistema modelado ante la dinámica y los cambios del entorno.
Esta modelación permite algunas ventajas frente a la problemática de la vida real. En primer lugar y para la mayoría de los casos, la simulación es menos costosa que la experimentación en la vida real. Otras ventajas tienen que ver con la posibilidad de observar el comportamiento de los sistemas modelados ante situaciones cambiantes de experimentación para entender sus procedimientos internos y estudiar las características de la evolución de estos modelos permitiendo anticipar las condiciones cambiantes de la vida real, tal como lo enuncia la Teoria General de Sistemas de Von Bertalanffy (1976).
Una tipología muy común de modelos de simulación se desarrolló a finales de la primera mitad del siglo XX y se le denominó Método Monte Carlo, el cual es un modelo estocástico que se basa en la generación de números aleatorios que pretenden simular el comportamiento de los agentes o variables que interactúan en un problema determinado de la vida real, cuyo procedimiento también es aleatorio. Este método simula la aleatoriedad del comportamiento de estas variables por medio de la generación de números contenidos dentro de unos parámetros específicos.
La utilidad de la simulación bajo el método Monte Carlo se basa en la posibilidad de utilizar la aleatoriedad del proceso como un proxy de los niveles de incertidumbre de la interacción de variables reales y su influencia o efecto sobre la variable dependiente a estimar, lo cual es una situación típica de la vida real (Mancilla, 2011). El proceso de generación de números seudo-aleatorios permite obtener resultados que se asemejan al comportamiento histórico de las variables analizadas, haciéndose posible de esta manera la construcción de la distribución de probabilidad en el problema analizado (Rubenstein y Kroese, 2008).
El origen de este método tiene que ver con la búsqueda de simulación de aleatoriedad y su aplicación se ha visto extendida en diferentes campos. Hacia 1940, Estanislaw Ulam se encontraba investigando en temas del desarrollo de la bomba atómica en el laboratorio de Los Álamos, para lo cual necesitaba predecir el comportamiento hidrodinámico de la difusión de neutrones, la cual por definición presenta comportamientos aleatorios. Ulam cuenta que la idea le surgió durante una incapacidad por enfermedad en la cual estaba jugando solitario, y mientras pensaba en cómo calcular la probabilidad de ganar reflexionó que era mucho más fácil cuantificar los resultados de una gran cantidad de intentos y analizar cuántas veces tenía éxito, que calcular las probabilidades anidadas de ocurrencia de cada tipo de carta. Creó entonces las bases de este método no determinista o estadístico numérico, trabajando posteriormente con John von Newman para refinar estos métodos utilizando equipos de cómputo. La utilización de herramientas informáticas facilitó la generación de números aleatorios y por lo tanto incrementaron la precisión de la estimación. Posteriormente a estos inicios, otros científicos tales como Harris, Herman Kahn, Enrico Fermi, Nicholas Metropolis y el mismo Ulam lograron desarrollos y aplicaciones más avanzadas de este método de simulación en campos tales como la fisión, la captura de neutrones a nivel nuclear, el comportamiento de las partículas subatómicas y la mecánica cuántica (Peña Sánchez, 2001).
El método de Montecarlo ofrece la posibilidad de obtener múltiples resultados con los mismos datos de entradas asegurando de este modo su aleatoriedad. Esta característica es útil para aproximar expresiones matemáticas complejas y costosas de evaluar con exactitud, lo que a su vez hace posible resolver problemas matemáticos mediante la simulación de variables aleatorias (Rodríguez-Aragón, 2011). Se basa, precisamente, en simular, repetir o duplicar durante una cierta cantidad de veces las características de un sistema real, de tal manera que se pueda predecir su comportamiento en las condiciones básicas o ante cambios controlados (Robert y Casella, 2004).
Es así como, en la actualidad, el método de simulación de Monte Carlo proporciona soluciones aproximadas a una gran variedad de problemas matemáticos posibilitando la realización de experimentos con muestreos de números seudoaleatorios en una computadora. El método es aplicable a cualquier tipo de problema, ya sea estocástico o determinista, lo que posibilita su aplicación en infinidad de casos relacionados con la teoría de los negocios y con la teoría de las organizaciones en prácticamente todos los casos asociados a problemas de la vida real. Como lo reportan Salazar y Alzate (2018), los ámbitos de aplicación de este sistema incluyen la administración, la ingeniería y la biología. Pero también es posible encontrar propuestas académicas más refinadas que incluyen la simulación de problemas econométricos (Ramírez y Ramírez, 2007), las finanzas y la investigación (Cruz, 2012; Vanalle, Lucato, Vieira y Sato, 2012) y de desarrollo de las empresas (Corrar, 1993).
En general, la utilización del método Monte Carlo aplicado en la academia en relación al estudio de situaciones académicas con aplicabilidad a problemáticas de la vida real se convierte en una importante herramienta de gestión del riesgo. No solo porque su aplicación actual mediante el uso de algoritmos informáticos permite obtener prácticamente todo el espectro de posibles resultados a una situación real, sino porque también permite definir la función de probabilidad que los genera (Lledó y Rivarola, 2007).
Las lúdicas de aprendizaje se refieren a aquellas actividades relacionadas con el ludus o los juegos que se desarrollan en el aula de clases como estrategia para mejorar los procesos de aprendizaje de los estudiantes. Autores como Chipia (2011) los denominan juegos serios, siendo definidos así aquellos cuyo objetivo principal es la formación, antes que el entretenimiento, donde los participantes pueden asumir roles de rivalidad o cooperación para resolver conflictos del juego, y sus decisiones terminan reflejando la comprensión de los elementos esenciales de la temática a analizar (Camacho y Rojas, 2018).
Este tipo de abordajes de la enseñanza buscan alternativas a la metodología de enseñanza tradicional, retomando el juego como una de las primeras estrategias de aprendizaje de los seres humanos en edades tempranas y reconociéndolo como parte esencial de la vida y ligada por lo tanto a procesos de formación integral (Coloma, Juca y Celi, 2019). A partir de esa premisa, las estrategias lúdicas buscan que el estudiante aprenda jugando, potenciando sus habilidades y aprendiendo de una forma agradable y casi siempre divertida (Posada, 2014). Los juegos generan una relación directa entre conceptos abstractos y problemas presentes en el mundo real, permitiendo la simulación de escenarios en los cuales los participantes deben tomar decisiones, siendo su objetivo principal el de permitir a los estudiantes tener la posibilidad de aprender haciendo (Rojas y Londoño, 2015).
Este tipo de aprendizaje activo despierta emociones, captura sensaciones y experiencias gracias a la participación activa del estudiante, definiendo una relación interactiva con el objeto de conocimiento, en algunos casos asumiendo retos progresivos que mejoran el proceso de aprendizaje y generan recordación de largo plazo (Cabezas, Molina y Ricaurte, 2018). Dentro de las diversas ventajas del uso del juego como estrategia de aprendizaje, se pueden encontrar las siguientes:
Estas ventajas se hacen particularmente útiles cuando el contenido del aprendizaje tiene un componente matemático importante. Las prevenciones que genera el proceso de enseñanza-aprendizaje de las matemáticas han sido objeto de estudio desde hace décadas, pues para una parte importante de los estudiantes esta faceta de sus estudios se convierte en un motivo de frustraciones y sentimientos autodepreciativos (Riviere, 1990), con el agravante de que sus creencias acerca de sus propias capacidades afectan el proceso de enseñanza aprendizaje (Boyd, Foster, Smith y Boyd, 2014) y muchas personas terminan sufriendo de ansiedad acerca de las matemáticas (Goos, Smith y Thornton, 2008).
Por esa razón, en los cursos de Distribución de Recursos e Investigación de Operaciones de la Universidad de Bogotá Jorge Tadeo Lozano estamos implementando estrategias lúdicas como motores de un aprendizaje dinámico y divertido, que promueva recordación significativa y a largo plazo de los conceptos principales de sus contenidos. En este caso, presentamos los resultados de la implementación de una lúdica para la enseñanza-aprendizaje de los conceptos básicos de la Simulación de Montecarlo, la cual se complementa con ejercicios prácticos en hoja de cálculo y retos empresariales para implementar lo aprendido.
En la enseñanza de las matemáticas, las actividades didácticas que el docente plantea no son percibidas de la misma forma por todos sus estudiantes y la emociones que estas generen en cada uno de ellos dependerán de lo que sientan, cómo perciban al profesor, la asignatura y cómo se enfrenten a esta. Algunos expresan satisfacción, reto, alegría y ánimo; mientras que otros sienten desesperación, tristeza, desánimo y estrés, lo que puede contribuir o afectar su aprendizaje. (Gamboa, 2014).
A partir del reto de impartir el tema de Simulación de Montecarlo, creamos un juego que busca dejar en los estudiantes el componente conceptual de su objetivo y su método de funcionamiento, el cual se basa en la repetición de simulaciones de unos resultados aleatorios que asemejan una situación real. La lúdica, denominada “Apuntando a la Simulación” fue luego aplicada en tres grupos de estudiantes y posteriormente se aplicó una evaluación por parte de 40 de ellos, quienes manifestaron sus impresiones y sugerencias con respecto a la actividad. A continuación se presenta la descripción del juego, el diseño muestral y la aplicación del instrumento de evaluación.
Nombre del juego |
Apuntando a la simulación |
||||||||||||||
Objetivo del juego |
Obtener un mayor puntaje total en los lanzamientos del tiro al blanco |
||||||||||||||
Materiales necesarios |
|
||||||||||||||
Propósitos educativos |
Generar apropiación de los conceptos básicos de la Simulación de Montecarlo y su aplicabilidad en áreas como la Investigación de Operaciones, el Cálculo y otras. |
||||||||||||||
No. de participantes |
Entre 10 y 50 participantes, organizados por grupos de 2 parejas |
||||||||||||||
Forma de organización del juego |
Los jugadores se agrupan por parejas y cada pareja tendrá una pareja rival. Es decir, en cada mesa habrá 4 jugadores y se jugará una “partida” independiente de las demás. |
||||||||||||||
Reglas del juego |
|
||||||||||||||
Tablero |
|
||||||||||||||
Cierre de la lúdica |
AREAov1 = 100 cm2 * (120/200) = 60 cm2 |
Se realizó un estudio de tipo exploratorio cuyo objetivo es determinar la percepción de los estudiantes que participaron de la lúdica Apuntando a la Simulación, con respecto a lo útil, práctico y ameno de la actividad. Para ello se realiza un muestreo por conveniencia, el cual realiza la selección de los elementos de la muestra de acuerdo con la facilidad de acceso o la conveniencia para la investigación. Este tipo de metodología hace parte de los muestreos no probabilísticos o circunstanciales, los cuales, si bien no permiten definir valores de probabilidades de que los elementos de la muestra sean incluidos ni del error de muestreo, ni permite hacer inferencias estadísticamente representativas, sí pueden ofrecer resultados indicativos valiosos para el investigador en estudios exploratorios cuando el diseño muestral es objetivo y previene sesgos de medición (López & Mejía, 2018).
Se estableció entonces como población la totalidad de estudiantes de los cursos de Distribución de Recursos e Investigación de Operaciones de la carrera de Administración de Empresas de la Universidad de Bogotá Jorge Tadeo Lozano y la muestra correspondió a 40 estudiantes a los que se les aplicó un instrumento tipo encuesta, con 4 preguntas puntuales: i) Su nivel de interés durante el desarrollo de la lúdica fue…; ii) La lúdica fue desarrollada de modo claro y comprensible; iii) Al final de la lúdica, su nivel de comprensión de la temática de Simulación de Montecarlo fue…
La lúdica “Apuntando a la Simulación” se aplicó en tres diferentes grupos de estudiantes, correspondientes a los grupos de las asignaturas equivalentes a Investigación de Operaciones 1 y 2 de la carrera de Administración de Empresas de la Universidad de Bogotá Jorge Tadeo Lozano, así como con un grupo de estudiantes de Ingeniería Industrial de otras universidades que trabaja el tema de lúdicas de aprendizaje.
Los resultados de las evaluaciones realizadas por los participantes en la lúdica muestran que a la gran mayoría de ellos la actividad les pareció amena (4.87 sobre 5 puntos), clara y comprensible (4.8 sobre 5) y que mantuvo un nivel de interés alto (4.72 sobre 5). Con respecto al objetivo principal de la lúdica, el de generar una comprensión sobre la temática de la Simulación de Montecarlo, tuvo una calificación de 4.55 puntos sobre 5, donde 39 de los 40 participantes afirmaron haber adquirido una comprensión alta o muy alta del tema (Ver Figura 1).
Figura 1
Evaluaciones del juego
Apuntando a la Simulación
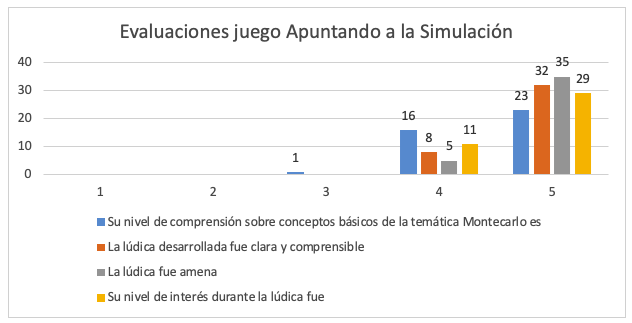
Adicionalmente, las opiniones cualitativas manifestadas por los estudiantes reflejan opiniones similares: “la lúdica fue amena”, “es mejor aprender así”, “fue una manera divertida de aprender”. Las sugerencias se concentraron especialmente en el componente estético del juego, tales como mejorar los dados, implementar un tablero imantado, hacer el tablero a todo color y otras. De la misma manera, hay sugerencias para darle más emoción al juego, como tener unas casillas de “peligro” en las cuales el jugador que caiga debe cumplir ciertas penitencias. Estas propuestas serán implementadas en próximas ediciones de la lúdica.
El estudio de caso presentado en este artículo se encuentra en concordancia con la revisión de la literatura acerca de las ventajas del uso de estrategias lúdicas de aprendizaje en el aula de clase. Ventajas que se relacionan entre otras con aspectos reportados en los resultados de este caso tales como aumento de los niveles de comprensión e interés hacia la asignatura u otros destacados como favorables en estrategias del proceso enseñanza-aprendizaje.
Las estrategias que se ven beneficiadas con el uso de estrategias lúdicas de aprendizaje en el aula tal y como ocurre en el presente caso, pueden caracterizarse bajo las categorías de estrategia afectiva, comunicativa, cognitiva y de memorización (Sánchez, 2010). En el caso de las estrategias afectivas se privilegia la cercana interacción entre el docente y el estudiante, el ambiente desinhibido y la actitud motivada del alumno. En el caso de las comunicativas se fortalece el intercambio no solo de información sino de argumentos entre las partes. En el caso de la cognitiva, aspecto en el que se logran los resultados más representativos se favorecen las competencias deductivas, de inferencia, de planteamiento de hipótesis, de comprobación o falsación y de estructura lógica. En cuanto a las de memorización, se cambia el paradigma de aprendizaje repetitivo por el de apropiación argumentada que permiten reproducir estructuras aprendidas y el uso de recursos nemotécnicos para aprender. Los resultados de las encuestas muestran que la lúdica utilizada respondió adecuadamente a estos parámetros. Los estudiantes encuestados la consideraron divertida, amena, que mantuvo su atención durante el desarrollo, pero también manifiestan que tuvieron un alto nivel de aprendizaje de los conceptos básicos de la temática de la Simulación de Montecarlo.
Aunque los resultados medidos en términos del aporte de la metodología a la comprensión de temáticas relacionadas con simulación bajo el Modelo Montecarlo en el caso de estudio analizado son muy alentadores en cuanto al aporte para los estudiantes, se considera importante profundizar y ampliar la aplicación de este tipo de dinámicas no solo en asignaturas relacionadas con simulación, sino en aquellas que involucren componentes de modelación de proyectos y de teoría de la decisión.
Por otra parte, vale la pena resaltar la conveniencia que tendría el poder realizar estas lúdicas de aprendizaje en el marco de una estrategia pedagógica que abarque más que el contenido de una asignatura, y pase a ser parte estructural de un programa académico. Es decir, que no dependa de un solo docente el uso del juego como estrategia de aprendizaje, sino que durante varias asignaturas se pueda utilizar este tipo de herramientas, pues se mostró durante la aplicación de esta y otras lúdicas que los estudiantes empiezan a desarrollar la capacidad de crear ellos mismos sus juegos para aprender, así como de ir generando propuestas para mejorar los juegos existentes. De alguna manera, puede decirse a partir de lo observado que el estudiante desarrolla su pensamiento “lúdico-académico” en la medida en que va utilizando estos juegos para aprender, de tal manera que cada vez más va desarrollando su pensamiento crítico hacia los juegos que le exponen y va mejorando su capacidad de crear lúdicas para el aprendizaje propio y el de sus compañeros, incluso cuando el profesor no utiliza este tipo de metodologías.
Tal y como se resalta en la discusión, el caso objeto de estudio permitió comprobar varios de los postulados referidos en la literatura como importantes al momento de proponer metodologías de aprendizaje en espacios académicos con alto contenido matemático y de modelación de la realidad.
Es precisamente esta característica la que permitiría generalizar el uso de estos métodos en niveles de formación tanto de pregrado como de posgrado, logrando un mayor compromiso y un alto nivel de percepción y entendimiento en este tipo de temáticas. Lo anterior se considera importante para aquellos segmentos de la población que tradicionalmente han presentado dificultades en el abordaje de temáticas con este tipo de contenidos.
Esta estrategia lúdica se debe complementar con ejercicios de aplicación práctica, con muestras de casos reales y talleres en Excel donde se aplique el método en temas de la Investigación de Operaciones, como la simulación de manejo de inventarios, el análisis de líneas de espera o la toma de decisiones en condiciones de incertidumbre. Un posible paso a seguir en esta investigación pedagógica sería evaluar la apropiación del tema a largo plazo, verificando que los conceptos básicos de la Simulación de Montecarlo hayan sido aprehendidos por los estudiantes y que esos conceptos les permitan aplicarlo a situaciones de la vida práctica de manera efectiva.
Acaso, M. (2010). La educación artística no son manualidades. Ed. Catarata.
Adams, M. (2016). Active Learning Strategies. Indiana: Indiana State University.
Arnab, S., Lim, T., Carvalho, M. B., Bellotti, F., de Freitas, S., Louchart, S., et al. (2015). Mapping learning and game mechanics for serious games analysis. British Journal of Educational Technology, 46(2), 391e411. http://dx.doi.org/10.1111/bjet.12113.
Bertalanffy, L. V., y Almela, J. (1976). Teoría general de los sistemas: fundamentos, desarrollo, aplicaciones. Fondo de Cultura Económica.
Boyd, Wendy; Foster, A.; Smith, J. & Boyd William (2014). Feeling Good about Teaching Mathematics: Addressing Anxiety amongst Pre-Service Teachers. Creative Education, 2014, 5, 207-217. http://dx.doi.org/10.4236/ce.2014.54030
Cabezas-Heredia, E.; Molina-Granja, F. y Ricaurte, P. S. (2018). Estrategia Lúdica para enseñanza en estudiantes de Ingeniería: Caso práctico. Revista Espacios. Volumen 40 (15), página 3. Recuperado de: http://www.revistaespacios.com/a19v40n15/a19v40n15p10.pdf
Camacho, S.K. y Rojas, M.D. (2018). Diseño de un juego serio para enseñar indicadores orientados a objetivos: RUMMICATORS. Revista Espacios. Volumen 39 (15), página 3. Recuperado de: https://www.revistaespacios.com/a18v39n15/18391510.html
Carvalho, M. B., Bellotti, F., Berta, R., De Gloria, A., Sedano, C. I., Hauge, J. B., … Rauterberg, M. (2015). An activity theory-based model for serious games analysis and conceptual design. Computers and Education, 87, 166–181. https://doi.org/10.1016/j.compedu.2015.03.023.
Chipia Lobo, J. F. (2011). Juegos serios: Alternativa innovadora. II Congreso en línea en Conocimiento Libre y Educación CLED2011, (pág. 18). Obtenido de http://erevistas.saber.ula.ve/index.php/cled/
Coloma, M. A.; Juca, J. M. y Celi, F. N. (2019). Estrategias metodológicas lúdicas de matemáticas en bachillerato general unificado. Revista Espacios. Volumen 40 (21), página 2. Recuperado de: http://www.revistaespacios.com/a19v40n21/a19v40n21p15.pdf
Corrar, L. J. (1993). O modelo econômico da empresa em condições de incerteza aplicação do método de simulação de Monte Carlo. Caderno de estudos, (8), 01-11.
Cruz, F. (2012). Procesos estocásticos en la valuación de proyectos de inversión, opciones reales, árboles binomiales, simulación bootstrap y simulación Monte Carlo: flexibilidad en la toma de decisiones. Contaduría y Administración, 57(2), 83-112.
Gamboa Araya, R. (2014). Relación entre la dimensión afectiva y el aprendizaje de las matemáticas. Revista Electrónica Educare. Volumen 18 (2), 117-139.
Goos, M., Smith, T., y Thornton, S. (2008). Research on the Pre-Service Education of Teachers of Mathematics. In H. Forgasz (Ed.), Research in Mathematics Education in Australasia 2004-2007. Rotterdam: The Netherlands Sense Publishers.
Lledó, P., y Rivarola, G. (2007). Gestión de proyectos. Buenos Aires: Prentice Hall - Pearson Educación.
López, D. C. y Mejía, L. (2014). Aplicación de una lúdica en el salón de clase para enseñanza de la ingeniería industrial. Caso Ingeniería de Métodos. Entre Ciencia e Ingeniería, Año 8. No. 15 – Primer Semestre de 2014, página 90 – 99.
Mancilla Herrera, A. M. (2011). Simulación Herramienta para el estudio de sistemas reales. Revista Científica Ingeniería y Desarrollo, (6), 104-112.
Peña Sánchez de Rivera, D. (2001). Deducción de distribuciones: el método de Monte Carlo. Fundamentos de Estadística. Alianza Editorial, Madrid. pp, 220-300.
Posada, R. (2014). La lúdica como estrategia didáctica. Universidad Nacional de Colombia. Recuperado de: http://www.bdigital.unal.edu.co/41019/1/04868267.2014.pdf
Ramírez, E. R., y Ramírez, P. A. R. (2007). Valor en riesgo: modelos econométricos contra metodologías tradicionales. Análisis económico, Volumen 22(51), 179-198.
Robert, C., y Casella, G. (2004). Monte Carlo Statistical Methods. Springer Science+Business Media. New York.
Rodrıguez-Aragón, L. J. (2011). Simulación, método de montecarlo. Recuperado de: https://previa.uclm.es/profesorado/licesio/docencia/mcoi/tema4_guion.pdf
Rojas, M.D. & Londono, L.M. (2013). Gestión del conocimiento para el sector real mediante juegos. Revista Puente Volumen 7, p.39-44.
Rubinstein, R. Y., & Kroese, D. P. (2016). Simulation and the Monte Carlo method (Vol. 10). John Wiley & Sons.
Salazar, E. y Alzate, W. (2018). Aplicación de la simulación Monte Carlo en la proyección del estado de resultados, un estudio de caso. Revista Espacios. Volumen 39 (51), 11-18.
Sánchez, G. (2010). Las estrategias de aprendizaje a través del componente lúdico. Revista de Didáctica Español Lengua Extranjera, (11), 1-68.
Santos, F.; Ferraz, D.F.; Klein, A.I. y Francisco, A.C. (2019). Jogo das três pistas: uma proposta lúdica para a avaliação dos subsunçores de genética. Revista Espacios. Volumen 39 (15), página 3. Recuperado de: https://revistaespacios.com/a19v40n05/a19v40n05p13.pdf
Tumay, K. (1996). Business process simulation. In Proceedings Winter Simulation Conference (pp. 93-98). IEEE.
Vanalle, R, Lucato, W., Vieira M. y Sato, I. (2012). Uso de la Simulación Monte Carlo para la Toma de Decisiones en una Línea de Montaje de una Fábrica. Información tecnológica, Volumen 23(4), 33-44. https://dx.doi.org/10.4067/S0718-07642012000400005
1. Universidad de Bogotá Jorge Tadeo Lozano. german.prieto@utadeo.edu.co
2. Universidad de Bogotá Jorge Tadeo Lozano. diegor.cabreram@utadeo.edu.co
[Índice]
revistaespacios.com

Esta obra está bajo una licencia de Creative Commons
Reconocimiento-NoComercial 4.0 Internacional